Spatio-Temporal

Misc

Packages
- {cubble} (Vignette) - Organizing and wrangling space-time data. Addresses data collected at unique fixed locations with irregularity in the temporal dimension
  - Handles sparse grids by nesting the time series features in a tibble or tsibble.
- {glmSTARMA} - (Double) Generalized Linear Models for Spatio-Temporal Data
- {magclass} - Data Class and Tools for Handling Spatial-Temporal Data
  - Has datatable under the hood, so it should be pretty fast for larger data
  - Conversions, basic calculations and basic data manipulation
- {mlr3spatiotempcv} - Extends the mlr3 machine learning framework with spatio-temporal resampling methods to account for the presence of spatiotemporal autocorrelation (STAC) in predictor variables
- {rasterVis} - Provides three methods to visualize spatiotemporal rasters:
  - hovmoller produces Hovmöller diagrams
  - horizonplot creates horizon graphs, with many time series displayed in parallel
  - xyplot displays conventional time series plots extracted from a multilayer raster.
- {SemiparMF} - Fits a semiparametric spatiotemporal (regression?) model for data with mixed frequencies, specifically where the response variable is observed at a lower frequency than some covariates.
  - Combines a non-parametric smoothing spline for high-frequency data, parametric estimation for low-frequency and spatial neighborhood effects, and an autoregressive error structure
- {sdmTMB} - Implements spatial and spatiotemporal GLMMs (Generalized Linear Mixed Effect Models)
- {sftime} - A complement to {stars}; provides a generic data format which can also handle irregular (grid) spatiotemporal data
- {spStack} - Bayesian inference for point-referenced spatial data by assimilating posterior inference over a collection of candidate models using stacking of predictive densities.
  - Currently, it supports point-referenced Gaussian, Poisson, binomial and binary outcomes.
  - Highly parallelizable and hence, much faster than traditional Markov chain Monte Carlo algorithms while delivering competitive predictive performance
  - Fits Bayesian spatially-temporally varying coefficients (STVC) generalized linear models without MCMC
- {stdbscan} - Spatio-Temporal DBSCAN Clustering
- {spTimer} (Vignette) - Spatio-Temporal Bayesian Modelling
  - Models: Bayesian Gaussian Process (GP) Models, Bayesian Auto-Regressive (AR) Models, and Bayesian Gaussian Predictive Processes (GPP) based AR Models for spatio-temporal big-n problems
  - Depends on {spacetime} and {sp}
- {stars} - Reading, manipulating, writing and plotting spatiotemporal arrays (raster and vector data cubes) in ‘R’, using ‘GDAL’ bindings provided by ‘sf’, and ‘NetCDF’ bindings by ‘ncmeta’ and ‘RNetCDF’
  - Only handles full lattice/grid data
  - It supercedes the {spacetime}, which extended the shared classes defined in {sp} for spatio-temporal data. {stars} uses PROJ and GDAL through {sf}.
    - Easily convert spacetime objects to stars object with st_as_stars(spacetime_obj)
  - Has dplyr verb methods
Resources
- SDS, Ch.13
- Geodata and Spatial Regression, Ch. 14
- Spatial Modelling for Data Scientists, Ch. 10
- Spatio-Temporal Statistics in R (See R >> Documents >> Geospatial)
- Spatial and Temporal Statistics
  - It’s kind of a brief overview of spatial and temporal modeling separately. The spatio-temporal section at the end is also brief and pretty basic.
  - There are things such as HMMs and GPs that I’m not yet familar with which could be interesting.
Papers
- INLA-RF: A Hybrid Modeling Strategy for Spatio-Temporal Environmental Data
  - Integrates a statistical spatio-temporal model with RF in an iterative two-stage framework.
  - The first algorithm (INLA-RF1) incorporates RF predictions as an offset in the INLA-SPDE model, while the second (INLA-RF2) uses RF to directly correct selected latent field nodes. Both hybrid strategies enable uncertainty propagation between modeling stages, an aspect often overlooked in existing hybrid approaches.
  - A Kullback-Leibler divergence-based stopping criterion.
- Effective Bayesian Modeling of Large Spatiotemporal Count Data Using Autoregressive Gamma Processes
  - Introduces spatempBayesCounts package but evidently it hasn’t been publicly released yet
- Amortized Bayesian Inference for Spatio-Temporal Extremes: A Copula Factor Model with Autoregression
Notes from
- spacetime: Spatio-Temporal Data in R - It’s been superceded by {stars}, but there didn’t seem to be much about working with vector data in {stars} vignettes. So, it seemed like a better place to start for a beginner, and I think the concepts might transfer since the packages were created by the same people. Some packages still use sp and spacetime, so it could be useful in using with those packages
- Spatio-Temporal Interpolation using gstat
Recommended Workflow (source)
- Go from simple analysis to complex (analysis) to get a feel for your data first. A lot of times, you probably will not need to do a spatio-temporal analysis at all.
- Steps
  1. Run univariate/multivariate analysis while ignoring space and time variables
  2. Aggregate over locations (e.g. average across all time points for each location). Then run spatial analysis (e.g. spatial regression, kriging, etc.).
    - Looking for patterns, hotspots, etc.
    - group_by(location) |> summarize(median_val = median(val))
    - e.g. min, mean, median, or max depending on the project
  3. Aggregate over time (e.g. average across all locations for each time point). Then run time series analysis (e.g. moving average, arima, etc.).
    - Looking trend, seasonality, shocks, etc.
    - group_by(date) |> summarize(max_val = max(val))
  4. Select interesting or important locations (e.g. top sales store, crime hotspot) and run a time series analysis on that location’s data
  5. Select interesting or important time points (e.g. holiday, noon) and run a spatial analysis on that time point
  6. Run a spatio-temporal analysis

Terms

Anisotropy
- Spatial Anisotropy means that spatial correlation depends not only on distance between locations but also direction.
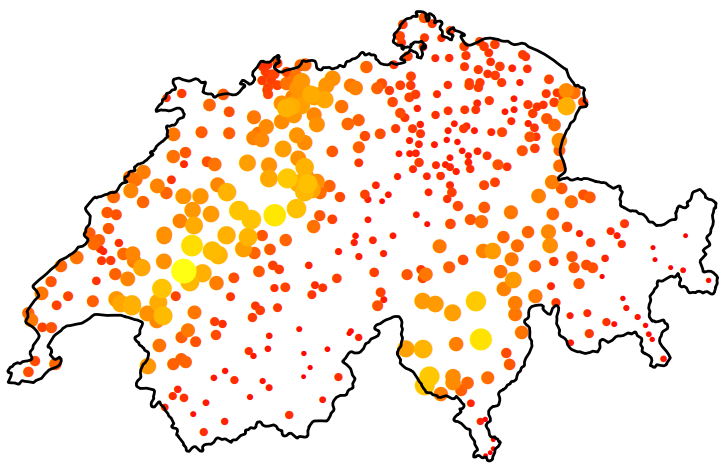
  - The size and color of circle represent rainfall values
  - The figure (source) demonstrates spatial anisotropy with alternating stripes of large and small circles from left to right, southwest to northeast.
  - Standard Kriging assumes isotropy (uniform in all directions) and uses an omnidirectional variogram that averages spatial correlation across all directions. Violation of isotropy can bias predictions; overestimate uncertainty in “stronger” directions (and vice versa); and the predictions will fail to capture patterns.
- Spatio-Temporal Anisotropy refers to directional dependence in correlation that varies across both space and time dimensions
  - Example: If you are mapping a pollution plume moving North at 10 km/h, the correlation structure is not just “longer in the North-South direction.”
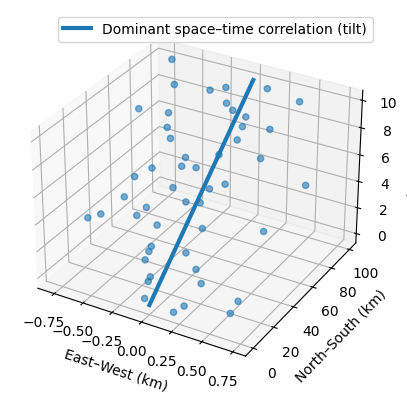
    - It is tilted in the space-time cube where time is the vertical in the 3d representation.
      - A vertical correlation (no anisotropy) would start at the bottom of the line and be parallel to the z-axis (time)
    - If you are measuring something that doesn’t move—like soil quality at a specific GPS coordinate—the time correlation is vertical
    - With a pollution plume, the time correlation will “tilt” because pollution values will be more similar in different locations as time increases.
Non-Spatial Microscale Effects - Sources of variability that do not necessarily decay with spatial distance over your sampling resolution, but appear as excess semivariance at short lags (i.e. possible explanations for a nugget effect)
- Measurement Error
  - Instrument noise
  - Calibration differences across monitors
  - Local siting effects (height, enclosure, nearby obstructions
- Sub-Grid Physical Variability
  - Street-level pollution vs background air
  - Near-road vs off-road effects
  - Local point sources (traffic lights, factories, heating units)
- Omitted Covariates
  - Elevation
  - Land use
  - Urban/rural classification
  - Meteorology (boundary layer height, wind exposure)
- Regime Mixing in Time
  - Seasonal transitions
  - Weather regimes
  - Policy or emissions changes
UNIX Time - The number of seconds between a particular time and the UNIX epoch, which is January the 1st 1970 GMT.
- Should have 10 digits. If it has 13, then milliseconds are also included.
- Convert to POSIXlt
```
data$TIME <- 
  as.POSIXlt(as.numeric(substr(
    paste(data$generation_time), start = 1, stope = 10)), 
    origin = "1970-01-01")
```
  - substr is subsetting the 1st 10 digits
  - paste is converting the numeric to a string. I’d try as.charater.

Grid Layouts

{spacetime} Classes
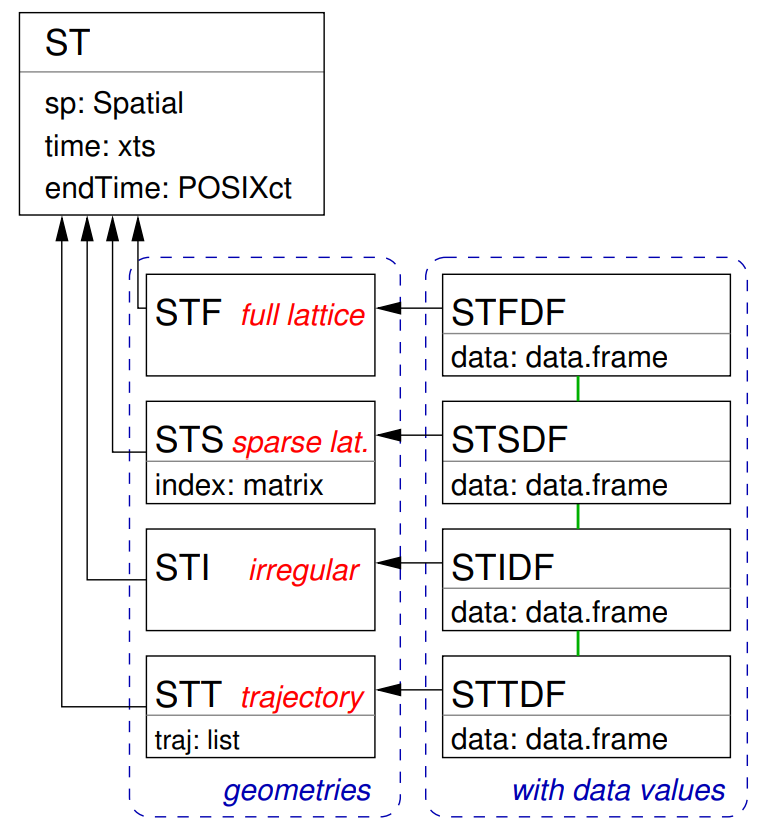
Full-Grids
- Each coordinate (spatial feature vs. time) for each time point has a value (which can be NA) — i.e. a fixed set of spatial entities and a fixed set of time points.
- Examples
  - Regular (e.g., hourly) measurements of air quality at a spatially irregular set of points (measurement stations)
  - Yearly disease counts for a set of administrative regions
  - A sequence of rainfall images (e.g., monthly sums), interpolated to a spatially regular grid. In this example, the spatial feature (images) are grids themselves.
Sparse Grids
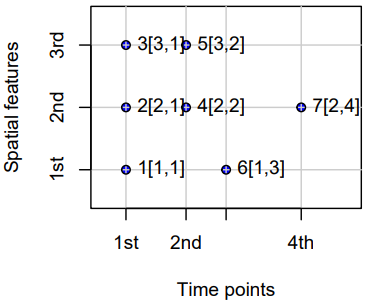
- Only coordinates (spatial feature vs. time) that have a value are included (no NA values)
- Use Cases
  - Space-time lattices where there are many missing or trivial values
    - e.g. grids where points represent observed fires, and points where no fires are recorded are discarded.
  - Each spatial feature has a different set of time points
    - e.g. where spatial feaatures are regions and a point indicates when and where a crime takes place. Some regions may have frequent crimes while others hardly any.
  - When spatial features vary with time
    - Scenarios
      - Some locations only exist during certain periods.
      - Measurement stations move or appear/disappear.
      - Remote sensing scenes shift or have different extents.
      - Administrative boundaries change (e.g., counties/tracts splitting or merging).
    - Example: Suppose you have monthly satellite images of vegetation over a region for three months
      - January: the satellite covers tiles A, B, and C
      - February: cloud cover obscures tile B; only A and C are available
      - March: a different orbital path covers B and D (a new area)
    - Example: Crime locations over time for a city
      - In 2018, you have GPS points for all recorded crimes that year (randomly scattered).
      - In 2019, you have a completely different set of GPS points (different crimes, different places).
      - The number of points per year also varies.
Irregular Grids
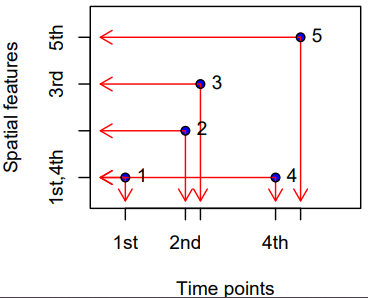
- Time and space points of measured values have no apparent organization: for each measured value the spatial feature and time point is stored, as in the long format.
- No underlying lattice structure or indexes. Each observation is a standalone (space, time) pair. Repeated values are possible.
- Essentially just a dataframe with a geometry column, datetime column, and value column.
- Use Cases
  - Mobile sensors or moving animals: each record has its own location and timestamp — no fixed grid or station network.
  - Lightning strikes: purely random events in continuous space-time.
Trajectory Grids
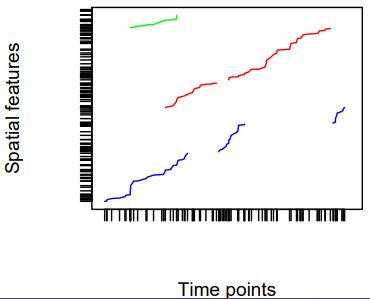
- Trajectories cover the case where sets of (irregular) space-time points form sequences, and depict a trajectory.
- Their grouping may be simple (e.g., the trajectories of two persons on different days), nested (for several objects, a set of trajectories representing different trips) or more complex (e.g., with objects that split, merge, or disappear).
- Examples
  - Human trajectories
  - Mobile sensor measurements (where the sequence is kept, e.g., to derive the speed and direction of the sensor)
  - Trajectories of tornados where the tornado extent of each time stamp can be reflected by a different polygon

Data Formats

Misc
- {spacetime} supported Time Classes: Date, POSIXt, timeDate ({timeDate}), yearmon ({zoo}), and yearqtr ({zoo})
- Data and Spatial Classes:
  - Points: Data having points support should use the SpatialPoints class for the spatial feature
  - Polygons: Values reflect aggregates (e.g., sums, or averages) over the polygon (SpatialPolygonsDataFrame, SpatialPolygons)
  - Grids: Values can be point data or aggregates over the cell.
- stConstruct creates “a STFDF (full lattice/full grid) object if all space and time combinations occur only once, or else an object of class STIDF (irregular grid), which might be coerced into other representations.”
- Latitude and Longitude to using {sp}
  - Example: (source)
    # Create a SpatialPointsDataFrame coordinates(df) <- ~ LON + LAT projection(df) <- CRS("+init=epsg:4326") # Transform into Mercator Projection # SpatialPointsDataFrame with coordinates in meters. ozone.UTM <- spTransform(df, CRS("+init=epsg:3395")) # SpatialPoints ozoneSP <- SpatialPoints(ozone.UTM@coords, CRS("+init=epsg:3395"))

Long - The full spatio-temporal information (i.e. response value) is held in a single column, and location and time are also single columns.

Example: Private capital stock (?)

#>     state year region     pcap     hwy   water    util       pc   gsp
#> 1 ALABAMA 1970      6 15032.67 7325.80 1655.68 6051.20 35793.80 28418
#> 2 ALABAMA 1971      6 15501.94 7525.94 1721.02 6254.98 37299.91 29375
#> 3 ALABAMA 1972      6 15972.41 7765.42 1764.75 6442.23 38670.30 31303
#> 4 ALABAMA 1973      6 16406.26 7907.66 1742.41 6756.19 40084.01 33430
#> 5 ALABAMA 1974      6 16762.67 8025.52 1734.85 7002.29 42057.31 33749

Each row is a single time unit and space unit combination.
This is likely not the row order you want though. I think these spatio-temporal object creation functions want ordered by time, then by space. (See Example)

Example: Create full grid spacetime object from a long table (7.2 Panel Data in {spacetime} vignette)

head(df_data); tail(df_data)
#>          state year region      pcap      hwy    water     util        pc    gsp    emp unemp
#> 1      ALABAMA 1970      6  15032.67  7325.80  1655.68  6051.20  35793.80  28418 1010.5   4.7
#> 18     ARIZONA 1970      8  10148.42  4556.81  1627.87  3963.75  23585.99  19288  547.4   4.4
#> 35    ARKANSAS 1970      7   7613.26  3647.73   644.99  3320.54  19749.63  15392  536.2   5.0
#> 52  CALIFORNIA 1970      9 128545.36 42961.31 17837.26 67746.79 172791.92 263933 6946.2   7.2
#> 69    COLORADO 1970      8  11402.52  4403.21  2165.03  4834.28  23709.75  25689  750.2   4.4
#> 86 CONNECTICUT 1970      1  15865.66  7237.14  2208.10  6420.42  24082.38  38880 1197.5   5.6
#>             state year region     pcap      hwy   water     util       pc   gsp    emp unemp
#> 731       VERMONT 1986      1  2936.44  1830.16  335.51   770.78  6939.39  7585  234.4   4.7
#> 748      VIRGINIA 1986      5 28000.68 14253.92 4786.93  8959.83 71355.78 88171 2557.7   5.0
#> 765    WASHINGTON 1986      9 41136.36 11738.08 5042.96 24355.32 66033.81 67158 1769.9   8.2
#> 782 WEST_VIRGINIA 1986      5 10984.38  7544.99  834.01  2605.38 35781.74 21705  597.5  12.0
#> 799     WISCONSIN 1986      3 26400.60 10848.68 5292.62 10259.30 60241.65 70171 2023.9   7.0
#> 816       WYOMING 1986      8  5700.41  3400.96  565.58  1733.88 27110.51 10870  196.3   9.0

yrs <- 1970:1986
vec_time <- 
  as.POSIXct(paste(yrs, "-01-01", sep=""), tz = "GMT")
head(vec_time)
#> [1] "1970-01-01 GMT" "1971-01-01 GMT" "1972-01-01 GMT" "1973-01-01 GMT" "1974-01-01 GMT" "1975-01-01 GMT"

head(spatial_geom_ids)
#> [1] "alabama"     "arizona"     "arkansas"    "california"  "colorado"    "connecticut"
class(geom_states)
#> [1] "SpatialPolygons"
#> attr(,"package")
#> [1] "sp"

The names of the objects above don’t the match the ones in the example, but I wanted names that were more informative about what types of objects were needed. The package documentation and vignette are spotty with their descriptions and explanations.
The row order of the spatial geometry object should match the row order of the spatial feature column (in each time section) of the dataframe.
The data_df only has the state name (all caps) and the year as space and time features.
spatial_geom_ids shows the order of the spatial geometry object (state polygons) which are state names in alphabetical order.
- At least in this example, the geometry object (geom_states) didn’t store the actual state names. It just used a id index (e.g. ID1, ID2, etc.)

st_data <- 
  STFDF(sp = geom_states, 
        time = vec_time, 
        data = df_data)

length(st_data)
#> [1] 816
nrow(df_data)
#> [1] 816
class(st_data)
#> [1] "STFDF"
#> attr(,"package")
#> [1] "spacetime"

df_st_data <- as.data.frame(st_data)
head(df_st_data[1:6]); tail(df_st_data[1:6])
#>           V1       V2 sp.ID       time    endTime timeIndex
#> 1  -86.83042 32.80316   ID1 1970-01-01 1971-01-01         1
#> 2 -111.66786 34.30060   ID2 1970-01-01 1971-01-01         1
#> 3  -92.44013 34.90418   ID3 1970-01-01 1971-01-01         1
#> 4 -119.60154 37.26901   ID4 1970-01-01 1971-01-01         1
#> 5 -105.55251 38.99797   ID5 1970-01-01 1971-01-01         1
#> 6  -72.72598 41.62566   ID6 1970-01-01 1971-01-01         1
#>             V1       V2 sp.ID       time    endTime timeIndex
#> 811  -72.66686 44.07759  ID44 1986-01-01 1987-01-01        17
#> 812  -78.89655 37.51580  ID45 1986-01-01 1987-01-01        17
#> 813 -120.39569 47.37073  ID46 1986-01-01 1987-01-01        17
#> 814  -80.62365 38.64619  ID47 1986-01-01 1987-01-01        17
#> 815  -90.01171 44.63285  ID48 1986-01-01 1987-01-01        17
#> 816 -107.55736 43.00390  ID49 1986-01-01 1987-01-01        17

So combining of these objects into a spacetime object doesn’t seemed be based any names (e.g. a joining variable) of the elements of these separate objects.
STFDF arguments:
- sp: An object of class Spatial, having n elements
- time: An object holding time information, of length m;
- data: A data frame with n*m rows corresponding to the observations
Converting back to a dataframe adds 6 new columns to df_data:
- V1, V2: Latitude, Longitude
- sp.ID: IDs within the spatial geomtry object (geom_states)
- time: Time object values
- endTime: Used for intervals
- timeIndex: An index of time “sections” in the data dataframe. (e.g. 1:17 for 17 unique year values)

Space-wide - Each space unit is a column

Example: Wind speeds

#>   year month day   RPT   VAL   ROS   KIL   SHA  BIR   DUB   CLA   MUL
#> 1   61     1   1 15.04 14.96 13.17  9.29 13.96 9.87 13.67 10.25 10.83
#> 2   61     1   2 14.71 16.88 10.83  6.50 12.62 7.67 11.50 10.04  9.79
#> 3   61     1   3 18.50 16.88 12.33 10.13 11.17 6.17 11.25  8.04  8.50
#> 4   61     1   4 10.58  6.63 11.75  4.58  4.54 2.88  8.63  1.79  5.83
#> 5   61     1   5 13.33 13.25 11.42  6.17 10.71 8.21 11.92  6.54 10.92
#> 6   61     1   6 13.21  8.12  9.96  6.67  5.37 4.50 10.67  4.42  7.17

Each row is a unique time unit

Example: Create full grid spacetime object from a space-wide table (7.3 Interpolating Irish Wind in {spacetime} vignette)

class(mat_wind_velos)
#> [1] "matrix" "array" 
dim(mat_wind_velos)
#> [1] 6574   12
mat_wind_velos[1:6, 1:6]
#>             RPT        VAL         ROS         KIL         SHA        BIR
#> [1,] 0.47349183  0.4660816  0.29476767 -0.12216857  0.37172544 -0.0549353
#> [2,] 0.43828072  0.6342761  0.04762928 -0.48431251  0.23530275 -0.3264873
#> [3,] 0.76797566  0.6297610  0.20133157 -0.03446898  0.07989186 -0.5358676
#> [4,] 0.01118683 -0.4751407  0.13684623 -0.78709720 -0.79381717 -1.1049744
#> [5,] 0.29298091  0.2851083  0.09805298 -0.54439303  0.02147079 -0.2707680
#> [6,] 0.27715281 -0.2860777 -0.06624749 -0.47759668 -0.66795421 -0.8085874

class(wind$time)
#> [1] "POSIXct" "POSIXt" 
wind$time[1:5]
#> [1] "1961-01-01 12:00:00 GMT" "1961-01-02 12:00:00 GMT" "1961-01-03 12:00:00 GMT" "1961-01-04 12:00:00 GMT" "1961-01-05 12:00:00 GMT"

class(geom_stations)
#> [1] "SpatialPoints"
#> attr(,"package")
#> [1] "sp"

See Long >> Example >> Create full grid spacetime object for a more detailed breakdown of creating these objects
The order of station geometries in geom_stations should match the order of the columns in mat_wind_velos
- In the vignette, the data used to create the geometry object is ordered according to the matrix using match. See R, Base R >> Functions >> match for the code.

st_wind = 
  stConstruct(
    # space-wide matrix
    x = mat_wind_velos, 
    # index for spatial feature/spatial geometries
    space = list(values = 1:ncol(mat_wind_velos)),
    # datetime column from original data
    time = wind$time, 
    # spatial geometry
    SpatialObj = geom_stations, 
    interval = TRUE
  )
class(st_wind)
#> [1] "STFDF"
#> attr(,"package")
#> [1] "spacetime"

df_st_wind <- as.data.frame(st_wind)
dim(df_st_wind)
#> [1] 78888     7
head(df_st_wind); tail(df_st_wind)
#>   coords.x1 coords.x2 sp.ID                time             endTime timeIndex     values
#> 1  551716.7   5739060     1 1961-01-01 12:00:00 1961-01-02 12:00:00         1  0.4734918
#> 2  414061.0   5754361     2 1961-01-01 12:00:00 1961-01-02 12:00:00         1  0.4660816
#> 3  680286.0   5795743     3 1961-01-01 12:00:00 1961-01-02 12:00:00         1  0.2947677
#> 4  617213.8   5836601     4 1961-01-01 12:00:00 1961-01-02 12:00:00         1 -0.1221686
#> 5  505631.2   5838902     5 1961-01-01 12:00:00 1961-01-02 12:00:00         1  0.3717254
#> 6  574794.2   5882123     6 1961-01-01 12:00:00 1961-01-02 12:00:00         1 -0.0549353
#>       coords.x1 coords.x2 sp.ID                time             endTime timeIndex    values
#> 78883  682680.1   5923999     7 1978-12-31 12:00:00 1979-01-01 12:00:00      6574 0.8600970
#> 78884  501099.9   5951999     8 1978-12-31 12:00:00 1979-01-01 12:00:00      6574 0.1589576
#> 78885  608253.8   5932843     9 1978-12-31 12:00:00 1979-01-01 12:00:00      6574 0.1536922
#> 78886  615289.0   6005361    10 1978-12-31 12:00:00 1979-01-01 12:00:00      6574 0.1325158
#> 78887  434818.6   6009945    11 1978-12-31 12:00:00 1979-01-01 12:00:00      6574 0.2058466
#> 78888  605634.5   6136859    12 1978-12-31 12:00:00 1979-01-01 12:00:00      6574 1.0835638

space has a confusing description. Here it’s just a numerical index for the number of columns of mat_wind_velos which would match an index/order for the geometries in geom_stations.
interval = TRUE, since the values are daily mean wind speed (aggregation)
- See Time and Movement section
df_st_wind is in long format

Time-wide - Each time unit is a column

Example: Counts of SIDS

#>          NAME BIR74 SID74 NWBIR74 BIR79 SID79 NWBIR79
#> 1        Ashe  1091     1      10  1364     0      19
#> 2   Alleghany   487     0      10   542     3      12
#> 3       Surry  3188     5     208  3616     6     260
#> 4   Currituck   508     1     123   830     2     145
#> 5 Northampton  1421     9    1066  1606     3    1197

SID74 contains to the infant death syndrome cases for each county at a particular time period (1974-1984). SID79 are SIDS deaths from 1979-84.
- NWB is non-white births, BIR is births.
Each row is a spatial unit and unique

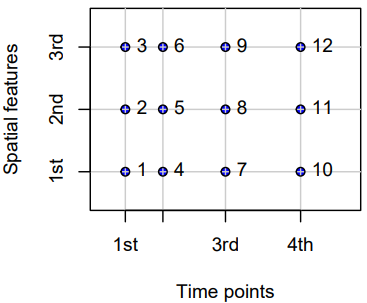
Time and Movement
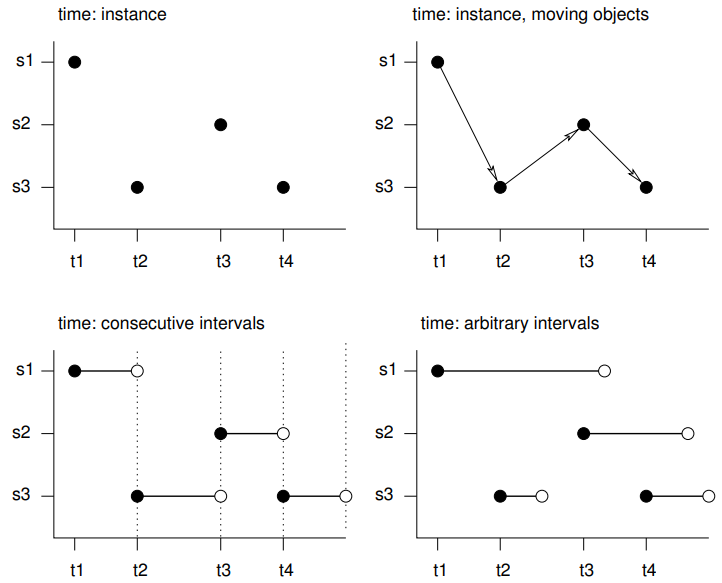
- s1 refers to the first feature/location, t1 to the first time instance or interval, thick lines indicate time intervals, arrows indicate movement. Filled circles denote start time, empty circles end times, intervals are right-closed
- Spatio-temporal objects essentially needs specification of the spatial, the temporal, and the data values
- Intervals - The spatial feature (e.g. location) or its associated data values does not change during this interval, but reflects the value or state during this interval (e.g. an average)
  - e.g. yearly mean temperature at a set of locations
- Instants - Reflects moments of change (e.g., the start of the meteorological summer), or events with a zero or negligible duration (e.g., an earthquake, a lightning).
- Movement - Reflects objects may change location during a time interval. For time instants. locations are at a particular moment, and movement occurs between registered (time, feature) pairs and must be continuous.
- Trajectories - Where sets of (irregular) space-time points form sequences, and depict a trajectory.
  - Their grouping may be simple (e.g., the trajectories of two persons on different days), nested (for several objects, a set of trajectories representing different trips) or more complex (e.g., with objects that split, merge, or disappear).
  - Examples
    - Human trajectories
    - Mobile sensor measurements (where the sequence is kept, e.g., to derive the speed and direction of the sensor)
    - Trajectories of tornados where the tornado extent of each time stamp can be reflected by a different polygon

EDA

Misc

Also see EDA, Time Series

Check for duplicate locations:

Kriging cannot handle duplicate locations and returns an error, generally in the form of a “singular matrix”.

Examples:

dupl <- sp::zerodist(spatialpoints_obj)

# sf
dup <- duplicated(st_coordinates(sf_obj))
log_mat <- st_equals(sf_obj)

# terra (or w/spatraster, spatvector)
d <- distance(lon_lat_mat)
log_mat <- which(d == 0, arr.ind = TRUE)

# base r
dup_indices <- duplicated(df[, c("lat", "long")])

# within a tolerance
# Find points within 0.01 distance
dup_pairs <- st_is_within_distance(sf_obj, dist = 0.01, sparse = FALSE)

General

Example: Days per Location

Code

library(dplyr); library(ggplot2)

data(DE_RB_2005, package = "gstat")
class(DE_RB_2005)
#> [1] "STSDF"

tibble(station_index = DE_RB_2005@index[,1]) |> 
  count(station_index) |> 
  ggplot(aes(x = station_index, y = n)) +
  geom_col(fill = "#2c3e50") + 
  scale_x_continuous(breaks = seq.int(0, length(unique(DE_RB_2005@index[,1])), 10)) +
  ylab("Number of Days") +
  ggtitle("Reported Days per Station") +
  theme_notebook()

# station names for some indexes w/low number of days
row.names(DE_RB_2005@sp)[c(4, 16, 52, 67, 68, 69)]
#> [1] "DEUB038"   "DEUB039"   "DEUB026"   "DEHE052.1" "DEHE042.1" "DEHE060"

If there’s there are locations with few observations on too many days, this can result in volatile variograms.

Example: Counts of pairwise distances between locations

Code

pacman::p_load(
  spacetime,
  sf,
  ggplot2
)

data(air)

# get rural location time series from 2005 to 2010
rural <- STFDF(
  sp = stations, 
  time = dates, 
  data = data.frame(PM10 = as.vector(air))
)
rr <- rural[,"2005::2010"]
# remove station ts w/all NAs
unsel <- which(apply(
  as(rr, "xts"), 
  2, 
  function(x) all(is.na(x)))
)
r5to10 <- rr[-unsel,]


sf_locs <- st_as_sf(r5to10@sp)
# Calculate pairwise distances
mat_dist_sf <- st_distance(sf_locs)
# Convert to kilometers
mat_dist_sf_km <- units::set_units(mat_dist_sf, km) |>
  units::drop_units()

dim(mat_dist_sf_km)
#> [1] 53 53

tibble::tibble(
  distance = mat_dist_sf_km[upper.tri(mat_dist_sf_km)]
) |> 
  ggplot(aes(x = distance)) +
  geom_histogram(
    binwidth = 20, 
    fill = "steelblue", 
    color = "#FFFDF9FF") +
  labs(x = "Distance (km)", y = "Frequency") +
  theme_notebook()

summary(mat_dist_sf_km[upper.tri(mat_dist_sf_km)])
#>   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>  7.027 197.849 308.533 321.976 439.895 813.742

The bin width is set to 20 km (which is the setting for the variogram model in the {gstat} vignette)
For kriging, ideally we’d want at least around 100 pairwise distances in each of the first few bins (short pairwise distances) for a stable range estimate, but no pairwise distance bin has that many. (See Geospatial, Kriging >> Bin Width)
- This is due to there only being 53 locations and the selection of only rural locations

Example: {gglinedensity}

Code

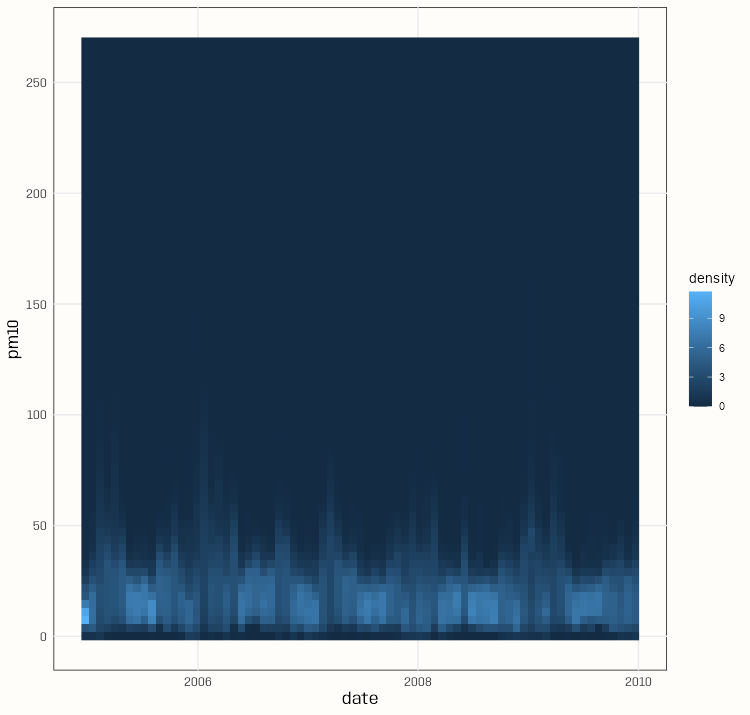
pacman::p_load(
  spacetime,
  dplyr,
  gglinedensity,
  ggplot2
)

data(air)

rural <- STFDF(
  sp = stations, 
  time = dates, 
  data = data.frame(PM10 = as.vector(air))
)
rr <- rural[,"2005::2010"]

# remove station ts w/all NAs
unsel <- which(apply(
  as(rr, "xts"), 
  2, 
  function(x) all(is.na(x)))
)
r5to10 <- rr[-unsel,]

pm10_tbl <- as_tibble(as.data.frame(r5to10)) |> 
  rename(station = sp.ID, date = time, pm10 = PM10) |> 
  mutate(date = as.Date(date)) |> 
  select(date, station, pm10)

summary(pm10_tbl)
#>       date               station           pm10        
#>  Min.   :2005-01-01   DESH001: 1826   Min.   :  0.560  
#>  1st Qu.:2006-04-02   DENI063: 1826   1st Qu.:  9.275  
#>  Median :2007-07-02   DEUB038: 1826   Median : 13.852  
#>  Mean   :2007-07-02   DEBE056: 1826   Mean   : 16.261  
#>  3rd Qu.:2008-10-01   DEBE032: 1826   3rd Qu.: 20.333  
#>  Max.   :2009-12-31   DEHE046: 1826   Max.   :269.079  
#>                       (Other):85822   NA's   :21979 

ggplot(
  pm10_tbl, 
  aes(x = date, 
      y = pm10,
      group = station)) +
  stat_line_density(
    bins = 75, 
    drop = FALSE, 
    na.rm = TRUE) + 
  scale_y_continuous(breaks = seq.int(0, 250, 50)) +
  theme_notebook()

With a bunch of time series, it’s difficult to distinguish a primary trend to the data (e.g. in a spaghetti line chart). This density gives a sense of the seasonality and the trend of most of the locations.
The summary says the median is around 14 and the max is around 270.

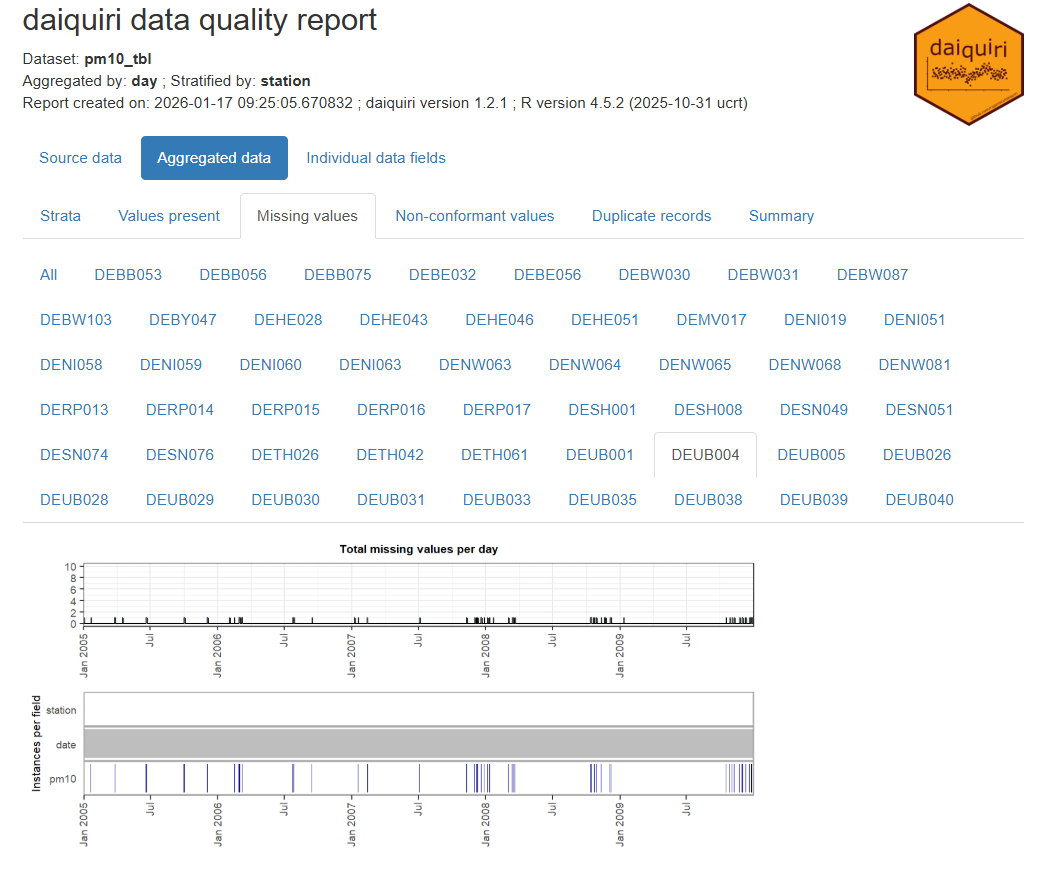
Example: {daiquiri}

Code

library(spacetime); library(dplyr); library(daiquiri)

data(air)

rural <- STFDF(
  sp = stations, 
  time = dates, 
  data = data.frame(PM10 = as.vector(air))
)
rr <- rural[,"2005::2010"]

# remove station ts w/all NAs
unsel <- which(apply(
  as(rr, "xts"), 
  2, 
  function(x) all(is.na(x)))
)
r5to10 <- rr[-unsel,]

pm10_tbl <- as_tibble(as.data.frame(r5to10)) |> 
  rename(station = sp.ID, date = time, pm10 = PM10) |> 
  mutate(date = as.Date(date)) |> 
  select(date, station, pm10)

fts <- 
  field_types(
    station = ft_strata(),
    date = ft_timepoint(includes_time = FALSE),
    pm10 = ft_numeric()
  )

daiq_pm10 <- 
  daiquiri_report(
    pm10_tbl,
    fts
  )

Shows missingness and basic descriptive statistics over time for each station
- Note that if your data is daily and there’s only 1 measurement per day, then all these statistics will the same (duh, but one time I forgot and thought the package was broken)

Autocorrelation

Check characteristics of autocorrelation. Can the analysis be done in a purely spatial manner (a purely spatial model for each time step) or is adding a temporal aspect necessary?
Autocorrelation Function (ACF)
- For each location, is there correlation between time $t$ and lag $t + h$
- Does autocorrelation rapidly or gradually decrease?
  - If gradually, then the series isn’t stationary and probably needs differencing (See EDA, Time Series >> Stationarity)
- Is there a scalloped shape to autocorrelation?
  - If so, it might need seasonal differencing.
- At which time lag (max, avg) does autocorrelation become insignificant?
Partial Autocorrelation Function (PACF)
- Are there significant spikes in the PACF?
  - Could indicate the frequency of the seasonality?
Cross-Correlations
- For each pair of locations, is there autocorrelation between location $a$ at time $t$ and location $b$ at time $t + h$
- Cross-correlations can be asymmetric and they do not have to 1 at lag 0 like autocorrelations
  - If you’re looking at rainfall at two locations, strong correlation when upstream location A leads downstream location B by 2 hours, but weak correlation when B “leads” A, tells you about the direction of storm movement and typical travel time.
  - The strength of the asymmetry itself (how different the two plots look) can indicate how strong or consistent these directional relationships are in your data.
- Potential Meaning Behind Strong Asymmetry:
  - Directional or causal relationships: If the cross-correlation is stronger when A leads B (positive lags in A vs B plot) than when B leads A, this suggests A might influence B more than the reverse. This doesn’t prove causation, but it’s often consistent with one variable driving changes in the other.S
  - Different response times: The asymmetry can reveal that one location responds to shared drivers faster than the other, or that the propagation time of some influence differs depending on direction.
  - Lead-lag relationships: Strong asymmetry with a clear peak at a non-zero lag indicates one series systematically precedes the other, which can be important for forecasting or understanding the physical mechanisms at play.
- Is there a approximate distance between many pairs of locations at which autocorrelation is insignificant?

Example: PM10 Pollution ({gstat} vignette, section 2)

Set-Up

pacman::p_load(
  spacetime,
  stars,
  sf,
  dplyr,
  ggplot2
)

data(air)

# get rural location time series from 2005 to 2010
rural <- STFDF(
  sp = stations, 
  time = dates, 
  data = data.frame(PM10 = as.vector(air))
)
rr <- rural[,"2005::2010"]

# remove station ts w/all NAs
unsel <- which(apply(
  as(rr, "xts"), 
  2, 
  function(x) all(is.na(x)))
)
r5to10 <- rr[-unsel,]

r5to10 is a STFDF (full grid) object
r5to10@sp is a SpatialPoints ({sp}) class object with location names and coordinates

Map

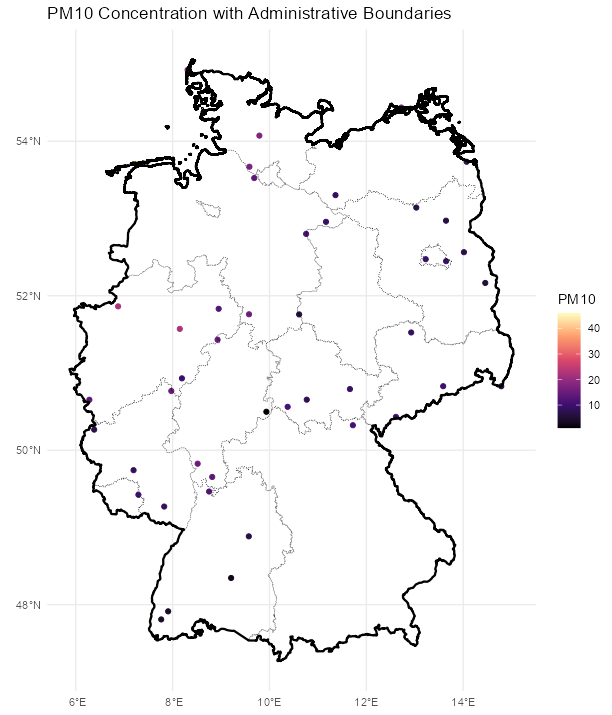
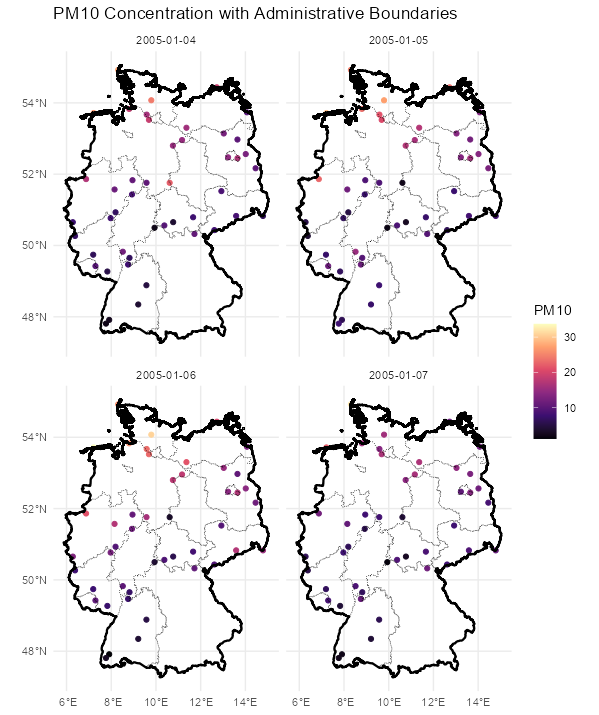
Code


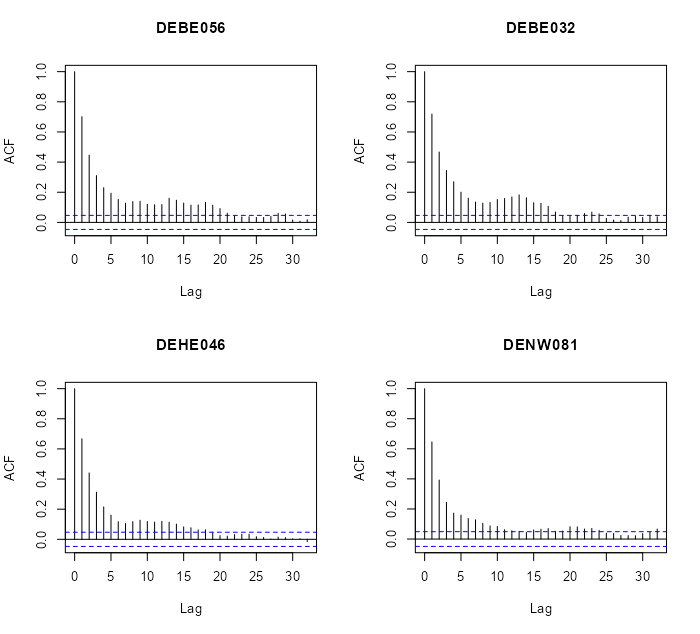
stars_r5to10 <- st_as_stars(r5to10)
# stars has dplyr methods
plot_slice <- 
  slice(stars_r5to10, 
        index = 3, # 3rd time step, so a location doesn't have NA 
        along = "time")
# country boundary
de_sf <- st_as_sf(DE)
# states (provinces) boundaries
nuts1_sf <- st_as_sf(DE_NUTS1)

ggplot() +
  # location points
  geom_stars(
    data = plot_slice, 
    aes(color = PM10), 
    fill = NA) +
  scale_color_viridis_c(
    option = "magma", 
    na.value = "transparent") +
  # states
  geom_sf(
    data = nuts1_sf, 
    fill = NA, 
    color = "black", 
    size = 0.2, 
    linetype = "dotted") +
  # country
  geom_sf(
    data = de_sf, 
    fill = NA, 
    color = "black", 
    size = 0.8) +
  # Ensures coordinates align correctly
  coord_sf() +
  labs(
    title = "PM10 Concentration with Administrative Boundaries",
    fill = "PM10"
  ) +
  theme_minimal()

# facet multiple time steps
plot_slices <- 
  slice(stars_r5to10, 
        index = 4:7, 
        along = "time")
plot_slices_sf <- st_as_sf(plot_slices, as_points = TRUE)
plot_slices_long <- 
  plot_slices_sf |> 
  pivot_longer(cols = !sfc, 
               names_to = "time", 
               values_to = "PM10")

ggplot() +
  geom_sf(
    data = plot_slices_long, 
    aes(color = PM10)) +
  scale_color_viridis_c(
    option = "magma", 
    na.value = "transparent") +
  geom_sf(
    data = nuts1_sf, 
    fill = NA, 
    color = "black", 
    size = 0.2, 
    linetype = "dotted") +
  geom_sf(
    data = de_sf, 
    fill = NA, 
    color = "black", 
    size = 0.8) +
  facet_wrap(~time) +
  coord_sf() +
  labs(
    title = "PM10 Concentration with Administrative Boundaries",
    color = "PM10"
  ) +
  theme_minimal()

# select locations 4, 5, 6, 7
rn = row.names(r5to10@sp)[4:7]

par(mfrow=c(2,2))
for (i in rn) {
  x <- na.omit(r5to10[i,]$PM10)
  acf(x, main = i)
}

There does seem to be a gradual-ness and scalloped pattern with these locations.
Looks like at around lag 20, autocorrelation is not significant for most of these locations

par(mfrow=c(2,2))
for (i in rn) {
  x <- na.omit(r5to10[i,]$PM10)
  pacf(x, main = i)
}

We see one or two significant spikes at each location, but nothing that would indicate a consistent seasonality among the locations.

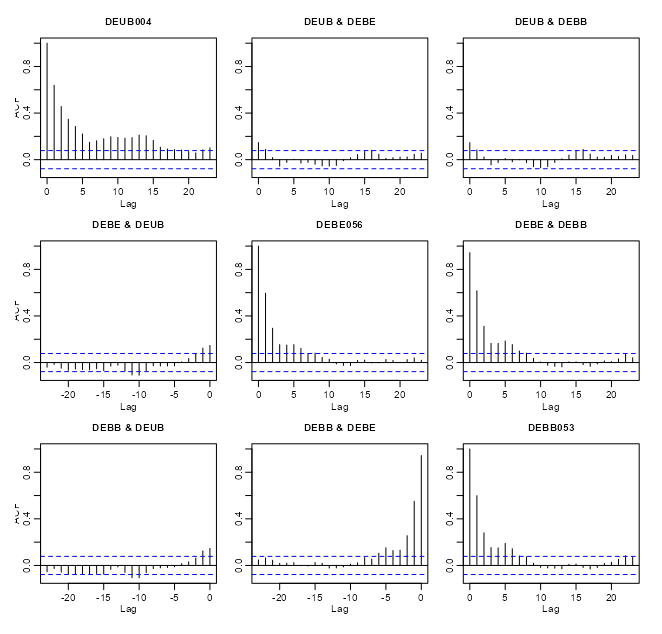
# coerce to xts class
xts_pm10 <- as(r5to10, "xts")
# extract numeric cols
mat_pm10 <- zoo::coredata(xts_pm10)
# find and remove cols with NAs > 20%
na_cols <- colnames(mat_pm10)[colMeans(is.na(mat_pm10)) > 0.20]
mat_pm10_nacols <- mat_pm10[, !colnames(mat_pm10) %in% na_cols]
mat_pm10_clean <- na.omit(mat_pm10_nacols)
# all data
acf(mat_pm10_clean)

# vs "DEUB004"
no_ac_locs <- c("DEUB004", "DEBE056", "DEBB053")
mat_pm10_naac <- mat_pm10_clean[, no_ac_locs]
acf(mat_pm10_naac)

r5to10 is a STFDF (full grid) object. It’s coerced, using as, into a xts object. Since it’s now a multivariate time series object, acf will give you cross-correlations.
From the acf of all the data, there were a couple interesting locations that had very little cross-correlation between them.
When running acf for a fairly large number of locations there will be a large number of charts (due to all the combinations). After one chart is rendered, in the R console, it’ll ask you to hit enter before it will render the next chart.
- Note that within the cross-correlation charts, the titles of some of the location names get cut off.

If there is no or little autocorrelation between a pair of locations, is it largely because there’s a large distance between those locations? Maybe this can give a hint about the appropriate neighborhood size or area

Distance Matrix

# select low cross-corr locations and random locations
# indices for the low cross-corr locations
no_ac_idx <- which(row.names(r5to10@sp) %in% no_ac_locs)
# indices for the column names (locations) of the cleaned matrix
mat_clean_idx <- which(row.names(r5to10@sp) %in% colnames(mat_pm10_clean))
# sample 5 location indices that aren't low cross-corr locations
mat_clean_idx_samp <- sort(sample(mat_clean_idx[-no_ac_idx], 5))
# combine sample indices and low cross-corr indices
mat_clean_idx_comb <- c(no_ac_idx, mat_clean_idx_samp)


# convert the SpatialPoints (sp) to sf
sf_locs <- st_as_sf(r5to10[mat_clean_idx_comb,]@sp)
# pairwise distances (in meters for geographic coordinates)
mat_dist_sf <- st_distance(sf_locs)
# convert to kilometers
mat_dist_sf_km <- round(units::set_units(mat_dist_sf, km), 2)

colnames(mat_dist_sf_km) <- row.names(r5to10[mat_clean_idx_comb,]@sp)
rownames(mat_dist_sf_km) <- row.names(r5to10[mat_clean_idx_comb,]@sp)
mat_dist_sf_km
#> Units: [km]
#>         DEBE056 DEBB053 DEUB004 DEBE056 DETH026 DEUB004 DEBW031 DENW068
#> DEBE056    0.00   28.07  648.60  235.43  357.82  541.62  198.99  557.63
#> DEBB053   28.07    0.00  674.84  256.26  374.67  569.64  221.21  585.50
#> DEUB004  648.60  674.84    0.00  441.77  660.90  209.86  579.71  173.85
#> DEBE056  235.43  256.26  441.77    0.00  458.62  393.98  292.91  396.71
#> DETH026  357.82  374.67  660.90  458.62    0.00  467.91  173.13  500.94
#> DEUB004  541.62  569.64  209.86  393.98  467.91    0.00  420.84   36.08
#> DEBW031  198.99  221.21  579.71  292.91  173.13  420.84    0.00  446.54
#> DENW068  557.63  585.50  173.85  396.71  500.94   36.08  446.54    0.00

# using sp
mat_dist_sp <- round(sp::spDists(r5to10[mat_clean_idx_comb,]@sp), 2)
colnames(mat_dist_sp) <- row.names(r5to10[mat_clean_idx_comb,]@sp)
rownames(mat_dist_sp) <- row.names(r5to10[mat_clean_idx_comb,]@sp)

The 3rd column (DEUB004) and first two rows (DEBE056, DEBB053) shows the distances between the low cross-correlation locations. The other locations are included for context.
The distances for those low cross-correlations location pairs do seem to be quite a bit larger than the other 5 randomly sampled locations when paired with DEUB004. So the low cross-correlations are likely due to larger spatial distances between the locations.
Might be interesting to check the cross-correlation between DEUB004 and DETH026 and maybe DEBW031 just to see how low those cross-correlations are in comparison.
The {sp} and {sf} numbers are slightly different, because {sp} uses spherical and {sf} uses elliptical distances. The elliptical should be more accurate, but either should be fine for most applications (fraction of a percentage difference)

Map

Code

labeled_points <- 
  st_as_sf(plot_slice, as_points = TRUE) |> 
  mutate(station = rownames(r5to10@sp@coords)) |> 
  filter(station %in% c("DEUB004", "DEBE056", "DEBB053"))

ggplot() +
  # location points
  geom_stars(
    data = plot_slice, 
    aes(color = PM10), 
    fill = NA) +
  scale_color_viridis_c(
    option = "magma", 
    na.value = "transparent") +
  # states
  geom_sf(
    data = nuts1_sf, 
    fill = NA, 
    color = "black", 
    size = 0.2, 
    linetype = "dotted") +
  # country
  geom_sf(
    data = de_sf, 
    fill = NA, 
    color = "black", 
    size = 0.8) +
  # Ensures coordinates align correctly
  coord_sf() +
  # color labelled points differently
  geom_sf(
    data = labeled_points, 
    color = "limegreen", 
    size = 3, 
    shape = 21, 
    fill = "limegreen") +
  geom_sf_label(
    data = labeled_points, 
    aes(label = station),
    nudge_x = 0.3, 
    nudge_y = 0.3, 
    size = 3) +
  labs(
    title = "PM10 Concentration with Administrative Boundaries",
    fill = "PM10") +
  theme_minimal()

Pretty much on the other side of the country, but there are locations further away. Again, it’d be interesting to look at the cross-correlations between some of the pairs of locations that are just as far or farther away.

Spatial Dependence

Is there meaningful spatial correlation at all (relative to noise)?
- Spatio-temporal variograms can appear structured even when spatial dependence is negligible—especially when temporal correlation is strong. So, we need to test whether spatial dependence exits independently.
- If there were no spatial correlation, then for almost all spatial lags (i.e. pure nugget behavior), semi-variance is constant.
- With spatial correlation, there should be a monotonic increase as distance increases which eventually plateaus.
  - Tells us that spatial dependence is not drowned out by temporal variability
On what distance scale does spatial correlation operate?
- At what distance does the variogram level off?
  - Realize the empirical range (calculated in the variogram model) and the practical range (using your eyes) are two different things.
- In general does this distance suggest a State-wide spatial dependence? County-wide? Region-wide? etc.
Is the spatial structure smooth or erratic?
- Can one curve fit the data well or are there groups of bins that stand out as not being fit well by the model curve.
- Does monotonicity of the bins fail? (i.e. a bin at greater distance than another but having a smaller semi-variance)
  - Try spatial detrending (e.g. regress on coordinates, covariates) or temporal detrending can restore a monotone variogram.
  - If variance or mean changes over time and you pool time slices, then differencing in time (or demeaning by time) can stabilize variance. Then, the short-lag spatial structure can become clearer.
Is fitting a full spatio-temporal variogram likely to succeed?
- Flat variogram → Don’t bother with spatial-temporal modeling when there’s no need for even spatial modeling.
- Extremely short range → Metric models likely degenerate.
- Wild instability → Spatio-Temporal fitting will be numerically meaningless. (too much noise → too much uncertainty → predictions essentially meaningless)

Example:

The data, r5to10, is PM10 measurements across 53 measurement stations in Germany. See EDA >> Autocorrelation >> Example 1 for details on this data.
Pooled spatial variograms are analyzed. Spatial dependence is calculated per sampled time instance and pooled across all sampled time instances.
Bootstrap distributions for the partial sill and range are calculated. These could give us a potential range of starting values if we use the same model (exponential) in the spatio-temporal variogram.

pacman::p_load(
  spacetime,
  gstat,
  tidyverse,
  futurize
)

# sample 100 time instances (days)
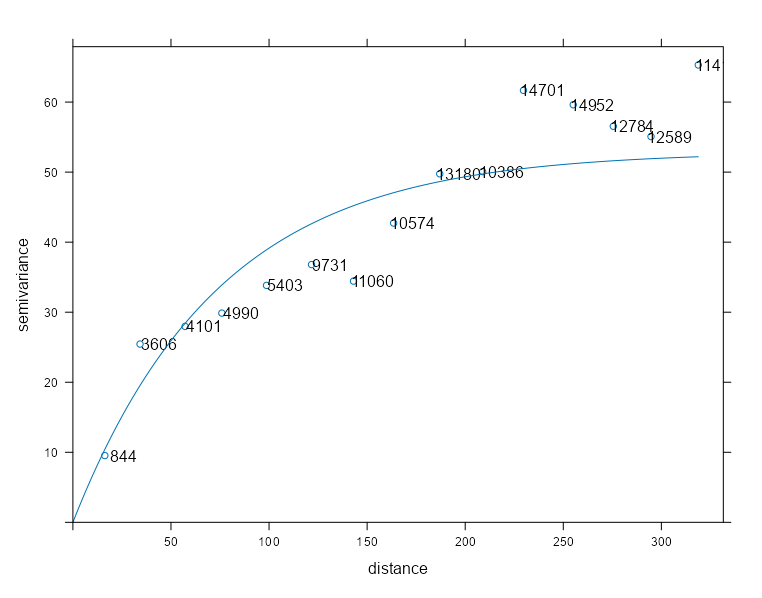
vec_time <- sample(
  x = dim(r5to10)[2],
  size = 100 # also used 300
)

ls_samp <- lapply(
  vec_time,
  function(i) {
    x = r5to10[,i]
    x$time_index = i
    rownames(x$coords) = NULL
    x
  }
)

spdf_samp <- do.call(
  what = rbind,
  args = ls_samp
)

100 time instances (days) are sampled
For each time instance, the STFDF is subsetted by that day. Then that day is added to a new variable, time_index.
Each element of ls_samp is a SpatialPointsDataFrame and rbind combines the elements into one SpatialPointsDataFrame

vario_samp <- 
  variogram(
    object = PM10 ~ time_index,
    locations = spdf_samp[!is.na(spdf_samp$PM10),],
    dX = 0
  )

mod_vario_samp_exp <- 
  fit.variogram(
    object = vario_samp, 
    model = vgm(
      psill = 100,
      model = "Exp",
      range = 200
    )
  )

mod_vario_samp_exp
#>   model    psill    range
#> 1   Exp 48.92291 51.20898

plot(
  x = vario_samp, 
  mod_vario_samp_exp, 
  plot.numbers = TRUE
)

The spatial variogram on the left uses 100 time slices (i.e. 100 days) and the one on the right uses 300.
The one on the left looks more unstable in the region (small distance pairs) where the range is estimated.
- Monotonicity is broken where the third bin has a lower semi-variance than the second bin.
- There is a large jump in semi-variance between the first and second bin.
In the one on right, monotonicity is restored and a smaller jump from bin 1 to bin 2 which results in a flatter fitted curve.
dX = 0 because including pairs from different time slices might have these effects:
- If temporal correlation is weak, short-distance bins inflate
- The estimated “spatial” range shrinks artificially
- The sill and nugget lose spatial interpretation
There are 53 locations, so choose(53, 2) says there 1,378 location pairs per time slice. Therefore, sampling 100 time instances means there are 13,780 pairs overall used to calculate this empirical variogram.
While this seems like a lot of data, it doesn’t fundamentally give us more spatial information about the area. Whether we sample 100 or use all the time slice to calculate the empirical variogram, the salient spatial variable is the number of locations which is just 53.
More time slices gives less variance (smoother line) to our model’s estimate of the psill and range, but doesn’t make it more accurate in terms of true “population” values. To increase the accuracy, we’d need more locations taking PM10 measurements.

After fitting variograms with a few different amounts of sampled time slices/instances a number of times, the variograms were substantially different — making it difficult to gain a feel for the partial sill and range parameters. Applying the bootstrap should give a better sense for a range of starting values for each of those parameters.
From the autocorrelation EDA example, there does seem to be some pretty strong autocorrelation present, so using the block version of bootstrapping makes sense. Probably could make blocks up to around 21 days judging by the ACFs, but I just went with 14 days here.
- Note that cross-correlations are more of spatio-temporal calculation. Setting dX = 0, means we’re modeling spatial dependence within time slices and then pooling, so the ACF is more appropriate to base our block length off of.

Block Bootstrap the Partial Sill and Range

See Confidence and Prediction Intervals >> Bootstrapping >> Example 2: Block Bootstrap for more details on the code.

Code

# ---------- Model and Block Functions ---------- #

1estim_params_vgm <-
  function(idx_time_resamp,
           dat) {

    ls_dat <- lapply(
      idx_time_resamp, 
      function(i) {
        x <- dat[, i]
        x$time_index <- i
        rownames(x@coords) <- NULL
        x
      }
    )

    spdf <- do.call(rbind, ls_dat)
    spdf <- spdf[!is.na(spdf$PM10), ]

    vario_exp <- variogram(
      PM10 ~ time_index,
      spdf,
      dX = 0
    )

    vario_mod <- try(
      fit.variogram(
        vario_exp, 
        vgm(psill = 100, 
            "Exp", 
            range = 200)),
      silent = TRUE
    )

    if (inherits(vario_mod, "try-error"))
      return(c(NA, NA))

    tibble(
      psill = vario_mod$psill,
      range = vario_mod$range
    )
  }

make_block_indices <- 
  function(n_time, 
           time_slices, 
           block_length, 
           n_samples) {
  mat_idxs <- matrix(NA, nrow = n_samples, ncol = time_slices)

2  for (r in seq_len(n_samples)) {
    idx <- integer(0)

3    while (length(idx) < time_slices) {
      start <- sample(
        1:(n_time - block_length + 1),
        size = 1
      )
      idx <- c(idx, start:(start + block_length - 1))
    }

    mat_idxs[r, ] <- idx[seq_len(time_slices)]
  }
  return(mat_idxs)
}



# ---------- Run it ---------- # 
4
time_slices <- 300 # 300 days
block_length <- 14 # 2 weeks
n_samples <- 200 # 200 resamples

block_idxs <- make_block_indices(
  n_time = dim(r5to10)[2],
  time_slices = time_slices,
  block_length = block_length,
  n_samples = n_samples
)

plan(future.mirai::mirai_multisession, workers = 10L)

tib_vario_params <- purrr::map(
  asplit(block_idxs, 1),
  \(x) {
    estim_params_vgm(x, dat = r5to10)
  }
) |> 
  futurize() |> 
  list_rbind()

mirai::daemons(0)

1: The basically just functionalizes the part of the script in the previous tabs and extracts the psill and range parameters from the variogram model
2: Iterates through the number of bootstrap replicates specified by n_samples
3: Generates blocks until the length of the replicate reaches the fixed length (time_slices)
4: A matrix is created with make_block_indices where each row is indices of PM10 observations which are organized in blocks of 14 days. Each row of that matrix is fed into estim_parmas_vgm where a variogram model is fit. The calculated psill and range parameters of the fitted model are collected in a tibble

Results

summary(tib_vario_params)
#>      psill            range       
#>  Min.   : 22.43   Min.   : 27.00  
#>  1st Qu.: 40.79   1st Qu.: 53.54  
#>  Median : 50.84   Median : 68.48  
#>  Mean   : 55.30   Mean   : 73.89  
#>  3rd Qu.: 62.64   3rd Qu.: 87.91  
#>  Max.   :160.85   Max.   :357.72

sd(tib_vario_params$psill)
#> [1] 21.50009
sd(tib_vario_params$range)
#> [1] 32.32091

We have medians less than means, so skew is present
The variance of each distribution is quite large.

Visualize

Code

library(ggdist); library(patchwork)

notebook_colors <- unname(swatches::read_ase(here::here("palettes/Forest Floor.ase")))

tib_plot <- 
  tib_vario_params |> 
  pivot_longer(cols = everything(), names_to = "parameter") |> 
  group_split(parameter)

psill_plot <- ggplot(
  data = tib_plot[[1]],
  aes(y = parameter, 
      x = value, 
      fill = parameter)) +
  stat_slab(
    aes(thickness = after_stat(pdf*n)), 
    scale = 0.7) +
  stat_dotsinterval(
    side = "bottom", 
    scale = 0.7, 
    slab_linewidth = NA) +
  scale_x_continuous(position = "top") +
  scale_fill_manual(values = notebook_colors[[4]]) +
  xlab("Semi-Variance") +
  guides(fill = "none") +
  theme_notebook(
    axis.title.y = element_blank(),
    panel.border = element_rect(color = "#FFFDF9FF", 
                                fill = "#FFFDF9FF", 
                                linewidth = 1.5))

range_plot <- ggplot(
  data = tib_plot[[2]],
  aes(y = parameter, 
      x = value, 
      fill = parameter)) +
  stat_slab(
    aes(thickness = after_stat(pdf*n)), 
    scale = 0.7) +
  stat_dotsinterval(
    side = "bottom", 
    scale = 0.7, 
    slab_linewidth = NA) +
  scale_fill_manual(values = notebook_colors[[8]]) +
  xlab("Distance (km)") +
  guides(fill = "none") +
  theme_notebook(
    axis.title.y = element_blank(),
    panel.border = element_rect(color = "#FFFDF9FF", 
                                fill = "#FFFDF9FF", 
                                linewidth = 1.5))
psill_plot/range_plot

Both parameter distributions are right-skewed with some outliers
So if we were to create a grid a starting values, it could be pretty wide.
Maybe more than 300 days (out of 1826 days) for the number of sampled time instances (slices) would help, but this is likely do to there only being 53 stations taking measurements.

Kriging

Misc

Packages
- {gstat} - OG; Has idw and various kriging methods.
The added value of spatio-temporal kriging lies in the flexibility to not only interpolate at unobserved locations in space, but also at unobserved time instances.
- This makes spatio-temporal kriging a suitable tool to fill gaps in time series not only based on the time series solely, but also including some of its spatial neighbours.
A potential alternative to spatio-temporal kriging is co-kriging.
- Only feasible if the number of time replicates is (very) small, as the number of cross variograms to be modelled equals the number of pairs of time replicates.
- Co-kriging can only interpolate for these time slices, and not inbetween or beyond them. It does however provide prediction error covariances, which can help assessing the significance of estimated change parameters
The best fits of the respective spatio-temporal models might suggest different variogram families and parameters for the pure spatial and temporal ones.
Spatio-Temporal vs Purely Spatial
- By examining the spatio-temporal variogram plot, you
  - Example (gstat vignette): A temporal lag of one or a few days leads already to a large variability compared to spatial distances of few hundred kilometers, implying that the temporal correlation is too weak to considerably improve the overall prediction.
For large datasets
- Try local kriging (instead of global kriging) by selecting data within some distance or by specifying nmax (the nearest n observations). (See krigeST below)

Workflow

# calculate sample/empirical variogram
vario_samp <- variogramST()

# specify covariance model
mod_cvar <- vgmST()

# fit variogram model
vario_mod <- 
  fit.STVariogram(
    object = vario_samp,
    model = mod_cvar
  )

# run variogram diagnostics
attr(vario_mod, "optim")$value
plot(vario_mod)
plot(vario_samp, vario_mod, wireframe = T)

Variogram

`variogramST`

Docs
Fits the Empirical/Experimental Variogram
Evidently fitting this object can take a crazy amount of time even with moderately sized datasets. So, it’s recommended to utilize the parallelization option (cores)
- In this article, he used a dataset with 6734 rows, and the dude ran it overnight. He didn’t use the core argument though. It was published 2015, so it might not have been available.
cutoff - Spatial separation distance up to which point pairs are included in semivariance estimates
- Default: The length of the diagonal of the box spanning the data is divided by three.
tlags - Time lags to consider. Default is 0:15
- For STIDF data, the argument tunit is recommended (and only used in the case of STIDF) to set the temporal unit of the tlags.
- The number of time lags is multiplied by the number of spatial bins to get the total bins. So the fewer the better, if the situation allows it. Fewer might also reduce computation time.
- Seems like days are typical time unit is spatio-temporal data, so 15 lags might be a lot depending on what’s being measured.
- Using the ACFs to get an idea
twindow - Controls the temporal window used for temporal distance calculations.
- This avoids the need of huge temporal distance matrices. The default uses twice the number as the average difference goes into the temporal cutoff. (I think this means twice the max of tlags)
  - Reduces unnecessary pair construction
  - Lowers memory use
  - Therefore, speeding up computation
- The function will create time-distance pairs that aren’t necessary
  - Example: STFDF
    - If time = Jan 1, 2, 3, 4, 5, 6 and tlags is set to 0:3
    - By default, the function will create the distance pair 1,6 even though a lag of at most 3 days is all we care about.
    - Setting twindow = 3 makes sure pairs like (1,6) aren’t created.
- For STFDF cases, setting twindow = max(tlags) makes sense because any less and not all the desired tlags pairs get created and any more is meaningless because those pairs won’t be used in the semi-variance calculations.
- For STIDF cases, maybe there’s something like Jan 3.5 which represents noon on that day and you want the pair (0, 3.5) created where max(tlags) = 3. Not sure if that pair would be included in the semi-variance calculation or not though. Might require a special tunits specification or transformation or something.
width - The width of subsequent distance intervals into which data point pairs are grouped for semivariance estimates
- Default: The cutoff is divided into 15 equal lags
- Also see Geospatial, Kriging >> Bin Width
cores - Compute in parallel

`vgmST`

Docs
Specifies the variogram model function.
Misc
- See Geospatial, Modeling >> Interpolation >> Kriging >> Variograms >> Terms for descriptions of sill, nugget, and range.
- For vgm, you can just use vgm("exponential") and not worry about setting parameters like sill, nugget, etc. This might also be the case with vgmST. (See Geospatial, Models >> Interpolation >> Kriging >> Variograms>> Example 1)
- For space and time arguments, vgm is used to specify those models
Covariance Models
- Separable
  - Covariance Function: $C_{\text{sep}} = C_s(h)C_t(u)$
  - Variogram: $\gamma_{\text{sep}}(h, u) = \text{sill} \cdot (\bar \gamma_s (h) + \bar \gamma_t(u) - \bar\gamma_s(h)\bar\gamma_t(u))$
    - $h$ is the spatial step and $u$ is the time step
    - $\bar \gamma_s$ and $\bar \gamma_t$ are standardized spatial and temporal variograms with separate nugget effects and (joint) sill of 1
  - vgmST(stModel = "separable", space, time, sill)
  - Has a strong computational advantage in the setting where each spatial location has an observation at each temporal instance (STFDF without NAs)
- Product-Sum
  - Covariance Function: $C_{\text{ps}}(h,u) = kC_s(h)C_t(u) + C_s(h) + C_t(u)$
    - With $k \gt 0$ (Don’t confuse this with the kappa anisotropy correction below)
  - Variogram:
    \[ \begin{align} \gamma_{\text{ps}}(h,u) = \;&(k \cdot \text{sill}_t + 1)\gamma_s(h) + \\ &(k \cdot \text{sill}_s + 1)\gamma_t(h) -\\ &k\gamma_s(h)\gamma_t(u) \end{align} \]
  - vgmST(stModel = "productSum", space, time, k)
- Metric
  - Assumes identical spatial and temporal covariance functions except for spatio-temporal anisotropy
    - i.e. Requires both spatial and temporal models use the same family. (e.g. spherical-spherical)
  - Covariance Function: $C_m(h,u) = C_{\text{joint}}(\sqrt{h^2 + (\kappa \cdot u)^2})$
    - $C_{\text{joint}}$ says that the spatial, temporal, and spatio-temporal distances are treated equally.
    - $\kappa$ is the anisotropy correction.
      - It’s in space/time units so multiplying it times the time step, $u$, converts time into distance. This allows spatial distance and temporal “distance” to be used together in the euclidean distance calculation
      - e.g. $\kappa = 189 \frac{\text{km}}{\text{day}}$ says that 1 day is equivalent to 189 km.
  - Variogram: $\gamma_m(h,u) = \gamma_{\text{joint}}(\sqrt{h^2 + (\kappa \cdot u)^2})$
    - $\gamma_{\text{joint}}$ is any known variogram tha may generate a nugget effect
  - vgmST("metric", joint, stAni)
    - stAni: The anisotropy correction ($\kappa$) which is given in spatial unit per temporal unit (commonly m/s). For estimating this input, see estiStAni below. Also see Terms >> Anisotropy
- Sum-Metric
  - A combination of spatial, temporal and a metric model including an anisotropy correction parameter, $\kappa$
  - Covariance Function: $C_{sm}(h,u) = C_s(h) + C_t(u) + C_{\text{joint}}(\sqrt{h^2 + (\kappa \cdot u)^2})$
  - Variogram: $\gamma_{sm}(h,u) = \gamma_s(h) + \gamma_t(u) + \gamma_{\text{joint}}(\sqrt{h^2 + (\kappa \cdot u)^2})$
    - Where $\gamma_s$, $\gamma_t$, and $\gamma_{\text{joint}}$ are spatial, temporal and joint variograms with separate nugget-effects
  - vgmST("sumMetric", space, time, joint, stAni)
    - Using the simple sum-metric model as starting values for the full sum-metric model improves the convergence speed.
- Simple Sum-Metric
  - Removes the nugget effects from the three variograms in the Sum-Metric model
  - Variogram: $\gamma_{\text{sm}}(h,u) = \text{nug} \cdot \mathbb{1}_{h\gt0\; \vee \; u\gt0} + \gamma_s(h) + \gamma_t(u) + \gamma_{\text{joint}}(\sqrt{h^2 + (\kappa \cdot u)^2})$
    - Think the nugget indicator says only include the nuggect effect if h or u is greater than 0.
  - vgmST("simpleSumMetric", space, time, joint, nugget, stAni)

`fit.StVariogram`

Docs
Fits the variogram model using the empirical variogram (variogramST) and variogram model specification (vgmST)
Misc
- extractPar(model) can be used to extract the estimated parameters from the variogram model
Weighting Options
- Controls the weighing of the residuals between empirical and model surface
- tl;dr Even though 6 is the default, 7 seems like a sound statistical choice unless the data/problem makes another method make more sense.
- Adding Weights narrows down the spatial and temporal distances and introduces a cutoff.
  - This ensures that the model is fitted to the differences over space and time actually used in the interpolation, and reduces the risk of overfitting the variogram model to large distances not used for prediction.
- To increase numerical stability, it is advisable to use weights that do not change with the current model fit. (?)
- Terms
  - $N_j$ is the number of location pairs for bin $j$
  - $h_j$ is the mean spatial distance for bin $j$
  - $u_j$ is the mean temporal distance for bin $j$
- Primarily two categories of methods:
  - Equal-Bin - Have a 1 in the numerator which means only the denominator contributes
    - Each lag bin contributes roughly equally to the objective function, regardless of how many point pairs went into estimating that bin.
    - Consider with small datasets where $N_j$ does not vary much across bins or when a balanced structure is called for.
  - Precision-Weighted - Have $N_j$ in the numerator
    - Assumes bins with more location pairs provide more reliable empirical variogram estimates
    - Parameter estimates tend to be more stable and less sensitive to small, noisy bins.
    - Consider with moderate to large datasets with substantial variation in $N_j$
- Methods
  - fit.method = 6 (default) - No weights
  - 1 and 3: Greater importance is placed on longer pairwise distance bins
  - 2 and 10: Involve weights based on the fitted variogram that might lead to bad convergence properties of the parameter estimates.
  - 7 and 11: Recommended to include the value of sfAni otherwise it’ll use the actual fitted spatio-temporal anisotropy which can lead the model to not converge.
    - estiStAni can be used to estimate the stAni value
    - The spatio-temporal analog to the commonly used spatial weighting
    - Denominator referred to as the metric distance which is similar to the what’s used in the metric covariance model
    - 7 puts higher confidence in lags filled with many pairs of spatio-temporal locations, but respects to some degree the need of an accurate model for short distances, as these short distances are the main source of information in the prediction step
  - 3, 4, and 5: Kept for compatibility reasons with the purely spatial fit.variogram function
  - 8 downweights more heaviliy the large pairwise distance bins (prioritizes small distance pairwise locations)
  - 9 downweights more heavily the large pairwise time-distance bins (prioritizes small time-distance pairwise locations)
stAni: The spatio-temporal anisotropy that is used in the weighting. Might be missing if the desired spatio-temporal variogram model already has the stAni parameter
- See Terms >> Anisotropy, vgmST >> Metric, Sum Metric, and Simple Sum Metric
- Default is NA and will be understood as identity (1 temporal unit = 1 spatial unit)
  - Docs says this assumption is rarely the case so could be worth including to see if it improves performance
- Anisotropy Estimation Heuristics using estiStAni
  - method = “linear” - Rescales a linear model
  - method = “range” - Estimates equal ranges
  - method = “vgm” - Rescales a pure spatial variogram
  - method = “metric” - Estimates a complete spatio-temporal metric variogram model and returns its spatio-temporal anisotropy parameter.

Diagnostics

“The selection of a spatio-temporal covariance model should not only be made based on the (weighted) mean squared difference between the empirical and model variogram surfaces (attributes(fit_vario)$value), but also on conceptional choices and visual judgement of the fits. (plot(emp_vario, c(fit_vario1, fit_vario2, fit_vario3), wireframe = TRUE, all = TRUE))”
plot - Shows the sample and fitted variogram surfaces next to each other as colored level plots. (Docs)
- wireframe = TRUE creates a wireframe plot
- diff = TRUE plots the difference between the sample and fitted variogram surfaces.
  - Helps to better identify structural shortcomings of the selected model
- all = TRUE plots sample and model variogram(s) in single wireframes
Convergence output from optim
- method = “L-BFGS-B” is the default. It uses a limited-memory modification of the BFGS quasi-Newton method, and has been said not the be as robust as “BFGS” which is supposed to be the gold standard (thread). So if you have issues, “BFGS” may be worth a try.
- Get these by accessing the optim.out attribute from fit.StVariogram
```
fit_var <- fit.StVariogram(...)
attr_opt <- attributes(fit_var)$optim.out
```
- $convergence - The convergence code (guessing this just binary: converged or not converged (attr_opt$convergence)
- $message - Probably gives more details about “not converged” or maybe the time, eps, etc.
- $value - The mean of the (weighted) squared deviations (loss function) between sample and fitted variogram surface. (aka Weighted Mean Squared Error (wMSE))
Check the estimated parameters against the parameter boundaries and starting values
- Be prepared to set upper and lower parameter boundaries if, for example, the sill parameters returned are negative.

Convergence Help

Starting values can affect the results (hitting local optima) or even success of the optimization
- Using a starting value grid search might better asses the sensitivity of the estimates.
- Starting values can in most cases be read from the sample variogram.
- Parameters of the spatial and temporal variograms can be assessed from the spatio-temporal surface fixing the counterpart at 0.
  - Example: Inspection of the ranges of the variograms in the temporal domain, suggests that any station more than at most 6 days apart does not meaningfully contribute
- The overall spatio-temporal sill including the nugget can be deducted from the plateau that a nicely behaving sample variogram reaches for ’large’ spatial and temporal distances.
In some cases, you should rescale spatial and temporal distances to ranges similar to the ones of sills and nuggets using the parameter parscale.
- control = list(parscale=…) - Input a vector of the same length as the number of parameters to be optimized (See optim docs for details)
- See vignette for an example. They used the simple sum-metric model to obtain starting values for the full sum-metric model, and that improved the convergence speed of the more complex model.
  - There is a note in the discussion section about how this resulted in the more complex model being essentially the same as the simple model, but they tried other starting values and still ended up with the same result. So don’t freak if you get the same model.
- In most applications, a change of 1 in the sills will have a stronger influence on the variogram surface than a change of 1 in the ranges.

Interpolate

A joint distance is formulated in the same manner as the metric covariance model, and then used to find a subset of data with k-NN for a prediction location. The interpolation performs iteratively for each spatiotemporal prediction location with that local subset of data.
- Other methods (staged search) and (octant search) are briefly described in the vignette but not implemented in {gstat}
krigeST(formula, data, modelList, newdata)
- data - Original dataset (used to fit variogramST)
- modelList - Object returned from fit.StVariogram
- newdata - An ST object with prediction/simulation locations in space and time
  - Should contain attribute columns with the independent variables (if present).
- computeVar = TRUE - Returns prediction variances
  - fullCovariance = TRUE - Returns the full covariance matrix
- bufferNmax = 1 (default) - Used to increase the search radius for neighbors (e.g. 2 would be double the default radius.)
  - A larger neighbourhood is evaluated within the covariance model and the strongest correlated nmax neighbours are selected
  - If the prediction variances are large, then this parameter should help by gathering more data points.
- nmax - The maximum number of neighboring locations for a spatio-temporal local neighbourhood
stplot(preds) will plot the results
spat-temp vig
- Regular measurements over time (i.e. hourly, daily) motivate regular binning intervals of the same temporal resolution. Nevertheless, flexible binning boundaries can be passed for spatial and temporal dimensions. This allows for instance to use smaller bins at small distances and larger ones for large distances
- we could have fitted the spatial variogram for each day separately using observations from that day only. However, given the small number of observation stations, this produced unstable variograms for several days and we decided to use the single spatial variogram derived from all spatio-temporal locations treating time slices as uncorrelated copies of the spatial random field.
- A temporal lag of one or a few days leads already to a large variability compared to spatial distances of few hundred kilometres, implying that the temporal correlation is too weak to considerably improve the overall prediction.
- Further preprocessing steps might be necessary to improve the modelling of this PM10 data set such as for instance a temporal AR-model followed by spatio-temporal residual kriging or using further covariates in a preceding (linear) modelling step.
- Parameters of the spatial and temporal variograms can be assessed from the spatio-temporal surface fixing the counterpart at 0. (Done the spatial. How to do the temporal?)
- The prediction at an unobserved location with a cluster of observations at one side will be biased towards this cluster and neglect the locations towards the other directions. Similar as the quadrant search in the pure spatial case an octant wise search strategy for the local neighbourhood would solve this limitation. A simpler stepwise approach to define an n-dimensional neighbourhood might already be sufficient in which at first ns spatial neighbours and then from each spatial neighbour nt time instances are selected, such that
- Starting values can in most cases be read from the sample variogram
  - need to see if a st empirical variogram can be plotted (or printed?) and what can actually be gleaned from it
st vig
- spatio-temporal variogram settings
  - width = 20, cutoff = 200 → ~10 spatial bins
  - tlags = 0:15 → 16 temporal bins
  - you now have ~160 bins.
  - With more bins, you get more bins with few observations which causes
    - estimates become extremely noisy
    - fitting metric or separable models becomes unstable
  - Reducing tlags is a variance-control decision, not a bias decision
  - heatmap also shows little correlation (high variance) approaching lag 5 while spatial correlation remains pretty strong even at 200 km (see stat ninja video)

From post

For some reason the first model, generic separable model gets automatically discarded even though it has the lowest error.
Empircal variogram heatmap
```
plot(var,map=T) 
```

fit.StVariogram model comparison

# empirical vs model multi-line chart
# maybe use a par(c(4,2)) and loop
# maybe list + all = T will do it; might also need par
plot(var,separable_Vgm,map=F) 

# error (needs a loop and table)
attr(SimplesumMetric_Vgm, "MSE")

# wireframe
plot(var,list(separable_Vgm, prodSumModel_Vgm, metric_Vgm, sumMetric_Vgm, SimplesumMetric_Vgm),all=T,wireframe=T)

statninja vid
- vid 3 on st vig
  - Empirical variogram
    - cutoff and tlags specified
    - heatmap - plot(vario)
      - The shades of color are too hard to distinguish to get any sort of quality numeric estimate
    - line plot - plot(vario, map = FALSE)
      - 100 semi-variance (no spdep) at lag 4 at around 40km
      - Should 40 km be our spatial range starting value and 4 be out time range starting value?
  - Metric Model
    - starting values: psill, range, nugget = 0, stAni
    - heatmap - plot(vario, mod)
      - shows much more variability in the time axis than the spatial one
        
        really smooths out the colors in the spatial dimension.
      - Don’t really like it as a way to tell how well it fits the empirical variogram
    - no line chart
  - Separable
    - starting values: sill (overall) and psill, range, nugget (for time and space models)
      - weird that the psill and nugget add to 1 but the sill is set to 100
    - fit - boundaries (lower and upper) set - five parameters
    - heatmap comparison w/metric
      - less smoothing which better captures the empircal vario
    - 3d wireframe comparison
      - pretty difficult to make any kind of judgement either way
    - no line chart
  - specialized prediction plot looks mostly uninformative (weird ordering, no polys)
- vid 4 fires
  - convex hull
  - time only variogram
  - make sure there’s no kappa in the separable model
  - starting values
    - cutoff max?/2 of spdist
    - range
    - siil as var