brms

Misc

  • Packages
    • {chkptstanr} - Fit Bayesian models in Stan with checkpointing, that is, the ability to stop the HMC sampler at will, and then pick right back up where the sampler left off.
      • Custom Stan models can be fitted, or the popular package brms can be used to generate the Stan code.
      • This package is fully compatible with the R packages brms, posterior, cmdstanr, and bayesplot.
    • {IJSE} - Provides a function to calculate infinite-jackknife-based standard errors for fixed effects parameters in ‘brms’ models, handling both clustered and independent data. Also handles quantile regression.
  • Resources
  • How brms fits models
  • The marginal Sigma posterior distribution is the distribution of residuals 
  • Set-Up

    • Example (source)

      options(
  mc.cores = 4,
  brms.backend = "cmdstanr"
)

CHAINS <- 4
ITER <- 2000
WARMUP <- 1000
BAYES_SEED <- 1234
  • Sampling the posterior

    • Logistic

      # sampling the posterior
f <- 
  fitted(b3.1, 
        summary = F,            # says we want simulated draws and not summary stats 
        scale = "linear") %>%    # linear outputs probabilities 
  as_tibble() %>% 
  set_names("p")
  • Optimization
    • {cmdstanr} as the backend

      • In the brms model function

        backend="cmdstanr", stan_model_args=list(stanc_options = list("O1"))
        • stanc_options = list("O1") might be made default in a future update
        • See thread for details

      • Set using options: options(brms.backend = "cmdstanr"

  • Syntax Helpers
    • bf (doc) - An alias for brmsformula that lets you specify model formulas

Linear Regression

  • Example: lm, Cont ~ Cont (SR, Ch.4)

    b4.3 <-  brm(data = dat, family = gaussian,
      height ~ 1 + weight,
      prior = c(prior(normal(178, 100), class = Intercept),
                prior(normal(0, 10), class = b),
                prior(uniform(0, 50), class = sigma)),
      iter = 41000, warmup = 40000, chains = 4, cores = 4,
      seed = 4, backend = "cmdstanr",
)

  • Example: Multivariable, Cont ~ Cont + Cont (SR, Ch.5)

    b5.3 <-  brm(data = dat, family = gaussian,
      Divorce ~ 1 + Marriage_s + MedianAgeMarriage_s,
      prior = c(prior(normal(10, 10), class = Intercept),
                prior(normal(0, 1), class = b),
                prior(exponential(1), class = sigma)),
      iter = 2000, warmup = 1000, chains = 4, cores = 4,
      seed = 5, backend = "cmdstanr", file = "fits/b05.03")
    • Outcome = Divorce rate, Predictor 1 = state’s marriage rate, Predictor 2 = state’s median marriage age

  • Example: Binary/Cat, Cont ~ Binary (SR, Ch. 5)

    data(Howell1, package = "rethinking") 
d <- Howell1
d <-  d %>% 
  mutate(sex = ifelse(male == 1, 2, 1), # create index variable
        sex = factor(sex)) # transforming it into a factor tells brms it's indexed
b5.8 <-  brm(data = d, 
            family = gaussian, 
            height ~ 0 + sex, # "0 +" notation means calculate separate intercepts for each category
            prior = c(prior(normal(178, 20), class = b), 
                      prior(exponential(1), class = sigma)), 
            iter = 2000, warmup = 1000, chains = 4, cores = 4, 
            seed = 5, backend = "cmdstanr",
            file = "fits/b05.08")
print(b5.8)
    • For nominal variable, increase the s.d. of the α prior (as compared to the binary prior) “to allow the different to disperse, if the data wants them to.”
    • “I encourage you to play with that prior and repeatedly re-approximate the posterior so you can see how the posterior differences among the categories depend upon it.”

  • Example: Multi-Categorical, Cont ~ Cat + Cat (SR, Ch. 5)

    b5.11 <-  brm(data = d, 
      family = gaussian, 
      # bf() is an alias for brmsformula() that lets you specify model formulas
      bf(kcal.per.g_s ~ 0 + a + h, 
        a ~ 0 + clade, 
        h ~ 0 + house, 
        # tells brm we're using non-linear syntax
        nl = TRUE), 
      prior = c(prior(normal(0, 0.5), nlpar = a), 
                prior(normal(0, 0.5), nlpar = h), 
                prior(exponential(1), class = sigma)), 
      iter = 2000, warmup = 1000, chains = 4, cores = 4, 
      seed = 5, backend = "cmdstanr",
      file = "fits/b05.11")

    • (As of May 2022) When using the typical formula syntax with more than one categorical variable, {brms} drops a category from every categorical variable except for the first one in the formula.

    • {brms} was orginally designed to wrap Stan multi-level models w/lme4 syntax, so maybe that has something do with it.

    • Kurz has links and discussion in Section 5.3.2 of his ebook

  • Example: Interaction, continuous * categorical (SR, Ch.8)

    # same as coding for cat vars except adding a slope that is also conditioned on the index
b8.3 <- 
  brm(data = dd, 
      family = gaussian, 
      # bf = "brms formula"
      bf(log_gdp_std ~ 0 + a + b * rugged_std_c, 
        a ~ 0 + cid, 
        b ~ 0 + cid, 
        # nl = "nonlinear" syntax
        nl = TRUE), 
      prior = c(prior(normal(1, 0.1), class = b, coef = cid1, nlpar = a), 
                prior(normal(1, 0.1), class = b, coef = cid2, nlpar = a), 
                prior(normal(0, 0.3), class = b, coef = cid1, nlpar = b), 
                prior(normal(0, 0.3), class = b, coef = cid2, nlpar = b), 
                prior(exponential(1), class = sigma)), 
      iter = 2000, warmup = 1000, chains = 4, cores = 4, 
      seed = 8, backend = "cmdstanr",
      file = "fits/b08.03")
    • Categorical variable needs an interaction spec and an intercept (main effect) spec

  • Example: Interaction, continuous * continuous (SR, Ch.8)

    b8.5 <- 
  brm(data = d, 
      family = gaussian, 
      blooms_std ~ 1 + water_cent + shade_cent + water_cent:shade_cent, 
      prior = c(prior(normal(0.5, 0.25), class = Intercept), 
                prior(normal(0, 0.25), class = b, coef = water_cent), 
                prior(normal(0, 0.25), class = b, coef = shade_cent), 
                prior(normal(0, 0.25), class = b, coef = "water_cent:shade_cent"), 
                prior(exponential(1), class = sigma)), 
      iter = 2000, warmup = 1000, chains = 4, cores = 4, 
      seed = 8, backend = "cmdstanr",
      file = "fits/b08.05")

  • Example: Interaction, categorical * categorial (mc-stan question)(SR, Lecture 9 video, Ch. 11 Note)

    fit <-
  brm(bf(y ~ 0 + a + b + c,
        a ~ 0 + F1,
        b ~ 0 + F2,
        # this is the interaction
        c ~ (0 + F1) : (0 + F2),
        nl = TRUE),
    data = dat)

# interaction-only model (should include main effects)
brm_mod <- brm(data = ucb_01,
              family = bernoulli,
              bf(admitted ~ 0 + gd, 
                  # this is the interaction 
                  gd ~ (0 + gender) : (0 + dept), 
                  nl = TRUE), 
              prior = prior(normal(0,1), nlpar = gd), 
              iter = 2000, warmup = 1000, cores = 3, chains = 3, 
              seed = 10, backend = "cmdstanr")

Logistic Regression

  • Example: Logistic, cont ~ cat + cat (SR, Ch.11)

    b11_bern <- brm(data = dat_sim, 
                    family = bernoulli(link = "logit"), 
                    bf(admit ~ a + d, 
                      a ~ 0 + gid, 
                      d ~ 0 + dept, 
                      nl = TRUE), 
                    prior = c(prior(normal(0, 1), nlpar = a), 
                              prior(normal(0, 1), nlpar = d)), 
                    iter = 4000, warmup = 1000, cores = 4, chains = 4, 
                    seed = 11, backend = "cmdstanr")
print(b11_bern)
            Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
a_gidmale      -1.06      0.51    -2.05    -0.07 1.00    1765    2356
a_gidfemale    -0.97      0.50    -1.96    0.00 1.00    1758    2366
d_dept1        -1.54      0.51    -2.55    -0.54 1.00    1773    2419
d_dept2        -0.50      0.50    -1.46    0.48 1.00    1763    2249

b11.4_bin <-  brm(data = dat_sim,   
                  family = binomial, 
                  bf(admit | trials(1) ~ a + d, 
                      a ~ 0 + gid,   
                      d ~ 0 + dept, 
                      nl = TRUE), 
                  prior = c(prior(normal(0, 1), nlpar = a), 
                            prior(normal(0, 1), nlpar = d)), 
                  iter = 2000, warmup = 1000, chains = 4, cores = 4, 
                  seed = 11, backend = "cmdstanr")
print(b11_bin)
            Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
a_gidmale      -1.02      0.52    -2.05    0.01 1.01      702      832
a_gidfemale    -0.94      0.52    -1.98    0.06 1.01      688      808
d_dept1        -1.58      0.53    -2.60    -0.53 1.01      693      787
d_dept2        -0.53      0.52    -1.53    0.49 1.01      685      718
    • Slightly different results (100ths). I feel more comfortable using the bernoulli spec if it’s just a typical logistic regression.
    • The “1” in “|trials(1)” says that this is case-level data
      • Including a | bar on the left side of a formula indicates we have extra supplementary information about our criterion. In this case, that information is that each pulled_left value corresponds to a single trial (i.e., trials(1)), which itself corresponds to the  n = 1 in the model specification (above) for the outcome variable (e.g. pulled_left).
    • The rest of the brms specification is standard for having two categorial explanatory variables (e.g. actor, treatment) (see Ch.5 >> categoricals >> multiple nominal)
      • i.e. ingredients for Logistic Regression: family = Binomial and binary_outcome|trials(1)

  • Example: Multinomial Logistic Regression (SR, Ch. 11)

    b11.13io <- 
  brm(data = d,       
      # refcat sets the reference category to the 3rd level 
      family = categorical(link = logit, refcat = 3), 
      career ~ 1, 
      prior = c(prior(normal(0, 1), class = Intercept, dpar = mu1), 
                prior(normal(0, 1), class = Intercept, dpar = mu2)), 
      iter = 2000, warmup = 1000, cores = 4, chains = 4, 
      seed = 11, backend - "cmdstanr",
      file = "fits/b11.13io")
b11.13io
##              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS 
## mu1_Intercept    -2.01      0.15    -2.30    -1.73 1.00    3324    2631 
## mu2_Intercept    -1.53      0.12    -1.77    -1.29 1.00    2993    2768

    • as of brms 2.12.0, “specifying global priors for regression coefficients in categorical models is deprecated.” Meaning — if we want to use the same prior for both, we need to use the dpar argument for each

    • The reference level, refcat ,  was set to the 3rd level so the scores for the levels 1 and 2 are shown

      • Default is level 1.
      • Had we used the brms default and used the first level of “career” as the pivot (aka reference category), those lines would have instead been dpar = mu2 , dpar = mu3

    • These are the score values that we’d get if we centered all the scores at level 3’s score value

      • Nothing to infer from these. We want the probabilities which are in the next section.

    • Alternate ways to fit this model

      # verbose syntax
b11.13io_verbose <-
  brm(data = d, 
      family = categorical(link = logit, refcat = 3),
      bf(career ~ 1,
        mu1 ~ 1,
        mu2 ~ 1),
      prior = c(prior(normal(0, 1), class = Intercept, dpar = mu1),
                prior(normal(0, 1), class = Intercept, dpar = mu2)),
      iter = 2000, warmup = 1000, cores = 4, chains = 4,
      seed = 11,
      file = "fits/b11.13io_verbose")

# nonlinear syntax
b11.13io_nonlinear <-
  brm(data = d, 
      family = categorical(link = logit, refcat = 3),
      bf(career ~ 1,
        nlf(mu1 ~ a1),
        nlf(mu2 ~ a2),
        a1 + a2 ~ 1),
      prior = c(prior(normal(0, 1), class = b, nlpar = a1),
                prior(normal(0, 1), class = b, nlpar = a2)),
      iter = 2000, warmup = 1000, cores = 4, chains = 4,
      seed = 11,
      file = "fits/b11.13io_nonlinear")
      • The verbose (and nonlinear) syntax makes it clear that we are fitting k-1 models, since “career” has 3 categories
      • Had we used the brms default and used the first level of career as the pivot (aka reference category), those lines would have instead been mu2 ~ 1, mu3 ~ 1

Discrete Distribution Models

  • Binomial (SR Ch. 11)

    b11.6 <-
  brm(data = d_aggregated,
      family = binomial,
      bf(left_pulls | trials(18) ~ a + b,
        a ~ 0 + actor,
        b ~ 0 + treatment,
        nl = TRUE),
      prior = c(prior(normal(0, 1.5), nlpar = a),
                prior(normal(0, 0.5), nlpar = b)),
      iter = 2000, warmup = 1000, chains = 4, cores = 4,
      seed = 11, backend = "cmdstanr",
      file = "fits/b11.06")

    • Including a | bar on the left side of a formula indicates we have extra supplementary information about our criterion.

      • To fit an aggregated binomial model with brms, we augment the <criterion> | trials() syntax where the value that goes in trials() is either a fixed number, as in this case, or variable (e.g. trials(applications) ) in the data indexing the number of trials, n.

    • Can also use a logistic model, but need case-level data (e.g. 0/1)

      • Deaggregate count data into 0/1 case-level data
      data(UCBadmit, package = "rethinking")
ucb <- UCBadmit %>% 
  mutate(applicant.gender = relevel(applicant.gender, ref = "male"))

# deaggregate to 1/0
deagg_ucb <- function(x, y) {
  UCBadmit %>%
    select(-applications) %>%
    group_by(dept, applicant.gender) %>%
    tidyr::uncount(weights = !!sym(x)) %>%
    mutate(admitted = y) %>%
    select(dept, gender = applicant.gender, admitted)
}
ucb_01 <- purrr::map2_dfr(c("admit", "reject"),
                          c(1, 0),
                          ~ disagg_ucb(.x, .y)
)

  • Logistic (SR Ch. 11)

    full_mod <- brm(bf(admitted ~ 0 + g + d + gd, 
                  g ~ 0 + gender, 
                  d ~ 0 + dept, 
                  # this is the interaction 
                  gd ~ (0 + gender) : (0 + dept), 
                  nl = TRUE), 
                prior = c(prior(normal(0,1), nlpar = g),
                          prior(normal(0,1), nlpar = d),
                          prior(normal(0,1), nlpar = gd)),
                data = ucb_01,
                family = bernoulli,
                iter = 2000, warmup = 1000, cores = 3, chains = 3,
                seed = 10, backend = "cmdstanr")

  • Poisson (SR Ch. 11)

    # cat * cont interaction model 
b11.10 <- 
  brm(data = d, 
      family = poisson, 
      bf(total_tools ~ a + b * log_pop_std, 
        a + b ~ 0 + cid, 
        nl = TRUE), 
      prior = c(prior(normal(3, 0.5), nlpar = a), 
                prior(normal(0, 0.2), nlpar = b)), 
      iter = 2000, warmup = 1000, chains = 4, cores = 4, 
      seed = 11, backend = "cmdstanr",
      file = "fits/b11.10")

  • Ordinal

Non-linear

  • Example: Basis Splines (SR, Ch.4)

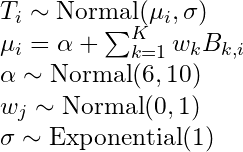
    # get recommended prior specifications
# s is the basis function brms imports from mgcv pkg
brms::get_prior(data = d2, 
                family = gaussian, 
                doy ~ 1 + s(year))
##                  prior    class    coef group resp dpar nlpar bound      source 
##                  (flat)        b                                          default 
##                  (flat)        b syear_1                            (vectorized) 
##  student_t(3, 105, 5.9) Intercept                                          default 
##    student_t(3, 0, 5.9)      sds                                          default 
##    student_t(3, 0, 5.9)      sds s(year)                            (vectorized) 
##    student_t(3, 0, 5.9)    sigma                                          default

# multi-level method
b4.11 <- brm(data = d2, 
            family = gaussian, 
            # k = 19, corresponds to 17 basis functions I guess ::shrugs:: 
            # The default for s() is to use what’s called a thin plate regression spline 
            # bs uses a basis spline 
            temp ~ 1 + s(year, bs = "bs", k = 19), 
            prior = c(prior(normal(100, 10), class = Intercept), 
                      prior(normal(0, 10), class = b), 
                      prior(student_t(3, 0, 5.9), class = sds), 
                      prior(exponential(1), class = sigma)), 
            iter = 2000, warmup = 1000, chains = 4, cores = 4, 
            seed = 4, backend = "cmdstanr",
            control = list(adapt_delta = .99))