Confidence & Prediction Intervals

Misc

  • Also see Mathematices, Statistics >> Descriptive Statistics >> Understanding CI, sd, and sem Bars
  • Packages
    • {SharpVarianceBounds} (Paper, Article) - Consistent estimate of the sharp variance bound for general regression-adjusted estimators of the average treatment effect in two-arm randomized controlled experiments
      • The way to estimate SATE of regressing the outcome on treatment group and covariates yields an unbiased estimate of the SATE; however, the standard error is a little too big, which means the confidence interval is a little too wide. The reason for this is that the correct standard error depends on the correlation between potential outcomes, but we cannot estimate a correlation between two variables if each trial participant only gives us one of the two values we wish to correlate.
  • SE used for CIs of the difference in proportion
    \[ \text{SE} = \sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}} \]
  • To obtain nonparametric confidence limits for means and differences in means, the bootstrap percentile method may easily be used and it does not assume symmetry of the data distribution.
  • CI Quantiles (Thread)
    • 66% and 95%
      • 66% is close to 66.6666% (i.e. the 2:1 odds interval)
      • 95% interval is roughly twice the width of the 66% on a normal distribution, which allows you to see kurtosis / fat tails when the intervals aren’t evenly spaced
    • 50%/80%/95% will be roughly evenly spaced on a normal if you need 3 intervals
  • Profile CIs
    • Also see
    • Unlike Wald CIs that rely on the normal distribution of the parameter estimate, profile CIs leverage the likelihood function of the model.
    • They essentially fix all the parameters in the model except the one of interest and then find the values for that parameter where the likelihood drops to a specific level. This level is determined by the desired confidence level (e.g., 95% CI).
    • Advantages
      • Applicable to a greater range of models
      • Generally more accurate than Wald CIs especially for smaller datasets
    • Preferred for:
      • Nonlinear models, complex models like mixed models, copulas, extreme value models, etc.
      • When the distribution of the parameter estimate is skewed or not normal.

Terms

  • Aleatoric Uncertainty (aka Stochastic Uncertainty) - Cannot be reduced by more knowledge; the random nature of a system, e.g. physical probabilities such as coin flips.
  • Confidence Intervals: A range of values within which we are reasonably confident the true parameter (e.g mean) of a population lies, based on a sample statistic (e.g. t-stat).

    • Frequentist Interpretation: The confidence interval is constructed by a procedure, which, if you were to repeat the experiment and collecting samples many many times, in 95% of the experiments, the corresponding confidence intervals would cover the true value of the population mean. (link)
      \[ [100\cdot(1-\alpha)]\;\%\: \text{CI for}\: \hat\beta_i = \hat\beta_i \pm \left[t_{(1-\alpha/2)(n-k)} \cdot \text{SE}(\hat\beta_i)\right] \]

      • \(t\) is the t-stat for
        • \(n-k\) = sample size - number of predictors
        • \(1-\alpha\) for 2-sided; \(1 - (\alpha/2)\) for 1 sided (I think)
      • \(\text{SE}(\beta_i)\) is the sqrt of the corresponding value on the diagonal of the variance-covariance matrix for the coefficients.

    • Bayesian Interpretation: the true value is in that interval with 95% probability

  • Coverage or Empirical Coverage: The level of coverage actually observed when evaluated on a dataset, typically a holdout dataset not used in training the model. Rarely will your model produce the Expected Coverage exactly
    • Adaptive Coverage: Setting your Expected Coverage so that your Empirical Coverage = Target Coverage. A conformal prediction algorithm is adaptive if it not only achieves marginal coverage, but also (approximately) conditional coverage
      • Example: 90% target coverage
        • If our model is slightly overfit, you might see that a 90% expected coverage leads to an 85% empirical coverage on a holdout dataset. To align your target and empirical coverage at 90%, may require setting expected coverage at something like 93%
    • Expected Coverage: The level of confidence in the model for the prediction intervals.
    • Conditional Coverage: The coverage for each individual class of the outcome variable or subset of data specified by a grouping variable.
    • Marginal Coverage: The overall average coverage across all classes of the outcome variable. All conformal methods achieve at or near the Expected Coverage averaged across classes but not necessarily for each individual class.
    • Target Coverage: The level of coverage you want to attain on a holdout dataset
      • i.e. The proportion of observations you want to fall within your prediction intervals
  • Epistemic Uncertainty (aka Systematic Uncertainty) - Can be reduced by more data, e.g. the uncertainty of estimated parameters
  • Jeffrey’s Interval: Bayesian CIs for Binomial proportions (i.e. probability of an event)

    • Example

      # probability of event
# n_rain in the number of events (rainy days)
# n is the number of trials (total days)
mutate(pct_rain = n_rain / n, 
       # jeffreys interval
       # bayesian CI for binomial proportions
       low = qbeta(.025, n_rain + .5, n - n_rain + .5), 
       high = qbeta(.975, n_rain + .5, n - n_rain + .5))
  • Prediction Interval: Used to estimate the range within which a future observation is likely to fall
    • Standard Procedure for computing PIs for predictions (See link for examples and further details)
      \[ \hat Y_0 \pm t^{n-p}_{\alpha/2} \;\hat\sigma \sqrt{1 + \vec x_0'(X'X)^{-1}\vec x_0} \]
      • \(Y_0\) is a single prediction
      • \(t\) is the t-stat for
        • \(n-p\) = sample size - number of predictors
        • \(1 - \alpha\) for 2-sided; \(1 - (\alpha/2)\) for 1 sided (I think)
      • \(\hat\sigma\) is the variance given by residual standard error, summary(Model1)$sigma
        \[ S^2 = \frac{1}{n-p}\;||\;Y-X\hat \beta\;||^2 \]
        • \(S = \hat \sigma\)
        • I think this is also the \(\operatorname{MSE}/\operatorname{dof}\) that you sometimes see in other formulas
      • \(x_0\) is new data for the predictor variable values for the prediction (also would need to include a 1 for the intercept)
      • \((X'X)^{-1}\) is the variance covariance matrix, vcov(model)

Diagnostics

  • Mean Interval Score (MIS)

    • (Proper) Score of both coverage and interval width
      • I don’t think there’s a closed range, so it’s meant for model comparison
      • Lower is better
    • greybox::MIS and (scaled) greybox::sMIS
      • Online docs don’t have these functions, but docs in RStudio do
    • Also scoringutils::interval_score
      • Docs have formula
        • The actual paper is dense Need to take the mean of MIS

  • Coverage

    • Example: Coverage %

      coverage <- function(df, ...){
  df %>%
    mutate(covered = ifelse(Sale_Price >= .pred_lower & Sale_Price pred_upper, 1, 0)) %>% 
    group_by(...) %>% 
    summarise(n = n(),
              n_covered = sum(
                covered
              ),
              stderror = sd(covered) / sqrt(n),
              coverage_prop = n_covered / n)
}
rf_preds_test %>% 
  coverage() %>% 
  mutate(across(c(coverage_prop, stderror), ~.x * 100)) %>% 
  gt::gt() %>% 
  gt::fmt_number("stderror", decimals = 2) %>% 
  gt::fmt_number("coverage_prop", decimals = 1)

    • Example: Test consistency of coverage across quintiles

      preds_intervals %>%  # preds w/ PIs
  mutate(price_grouped = ggplot2::cut_number(.pred, 5)) %>%  # quintiles
  mutate(covered = ifelse(Sale_Price >= .pred_lower & Sale_Price <= .pred_upper, 1, 0)) %>% 
  with(chisq.test(price_grouped, covered))
      • p value < 0.05 says coverage significantly differs by quintile
      • Sale_Price is the outcome variable

  • Interval Width

    • Narrower bands should mean a more precise model

    • Example: Average interval width across quintiles

      lm_interval_widths <- preds_intervals %>% 
  mutate(interval_width = .pred_upper - .pred_lower,
        interval_pred_ratio = interval_width / .pred) %>% 
  mutate(price_grouped = ggplot2::cut_number(.pred, 5)) %>% # quintiles
  group_by(price_grouped) %>% 
  summarize(n = n(),
            mean_interval_width_percentage = mean(interval_pred_ratio),
            stdev = sd(interval_pred_ratio),
            stderror = stdev / sqrt(n)) %>% 
  mutate(x_tmp = str_sub(price_grouped, 2, -2)) %>% 
  separate(x_tmp, c("min", "max"), sep = ",") %>% 
  mutate(across(c(min, max), as.double)) %>% 
  select(-price_grouped)

lm_interval_widths %>% 
  mutate(across(c(mean_interval_width_percentage, stdev, stderror), ~.x*100)) %>% 
  gt::gt() %>% 
  gt::fmt_number(c("stdev", "stderror"), decimals = 2) %>% 
  gt::fmt_number("mean_interval_width_percentage", decimals = 1)
      • Interval width has actually been transformed into a percentage as related to the prediction (removes the scale of the outcome variable)

Bootstrapping

  • Misc
    • Also see
    • Do NOT bootstrap the standard deviation
      • article
      • bootstrap is “based on a weak convergence of moments”
      • if you use an estimate based standard deviation of the bootstrap, you are being overly conservative (i.e. overestimate the sd)
    • bootstrapping uses the original, initial sample as the population from which to resample, whereas Monte Carlo simulation is based on setting up a data generation process (with known values of the parameters of a known distribution). Where Monte Carlo is used to test drive estimators, bootstrap methods can be used to estimate the variability of a statistic and the shape of its sampling distribution
    • Packages
  • Steps
    1. Resample with replacement
    2. Calculate statistic of resample
    3. Store statistic
    4. Repeat 10K or so times
    5. Calculate mean, sd, and quantiles for CIs across all collected statistics
  • CIs
    • Plenty of articles for means and models, see bkmks
    • rsample::reg_intervals is a convenience function for lm, glm, survival models
  • PIs
    • Bootstrapping PIs is a bit complicated
      • See Shalloway’s article (code included)
      • only use out-of-sample estimates to produce the interval
      • estimate the uncertainty of the sample using the residuals from a separate set of models built with cross-validation

Conformal Prediction Intervals

Misc

  • Packages
    • {{mapie}} - Handles scikit-learn, tf, pytorch, etc. with wrappers. Computes conformal PIs for Regression, Classification, and Time Series models.
      • Regression
        • Methods: naive, split, jackknife, jackknife+, jackknife-minmax, jackknife-after-bootstrap, CV, CV+, CV-minmax, ensemble batch prediction intervals (EnbPI).
        • “Since the typical coverage levels estimated by jackknife+ follow very closely the target coverage levels, this method should be used when accurate and robust prediction intervals are required.”
        • “For practical applications where N is large and/or the computational time of each leave-one-out simulation is high, it is advised to adopt the CV+ method” even though the interval width will be slightly larger than jackknife+
        • “The jackknife-minmax and CV-minmax methods are more conservative since they result in higher theoretical and practical coverages due to the larger widths of the prediction intervals. It is therefore advised to use them when conservative estimates are needed.”
        • “The conformalized quantile regression method allows for more adaptiveness on the prediction intervals which becomes key when faced with heteroscedastic data.”
        • EnbPI is for time series and residuals must be updated each time new observations are available
      • Classification

        • Methods: LAC, Top-K, Adaptive Prediction Sets (APS), Regularized Adaptive Prediction Sets (RAPS), Split and Cross-Conformal methods.

        • The difference between these methods is the way the conformity scores are computed

        • LAC method is not adaptive: the coverage guarantee only holds on average (i.e. marginal coverage). Difficult classification cases may have prediction sets that are too small, and easy cases may have sets that are too large. (See below for details on process). Doesn’t seem like to great a task to manually make it adaptive though (See example below).

        • APS’ conformity score used to determine the threshold is a constrained sum of the predicted probabilities for that observation. Only the predicted probabilites \(\ge\) the predicted probability of the true class are included in the sum. Everything else is the same as the LAC algorithm, although the default behavior is to keep the last class that crosses the threshold through the argument, include_last_label = [True, “randomized”, False]. The value of the argument can determine whether conditional coverage is (approximately) attained with True being the most liberal setting. Note that only “randomized” can produce empty predicted class sets. Algorithm tends to produce large predicted class sets when there are many classes in the outcome variable.

        • RAPS attenuates the lengthier predicted class sets in APS through regularization. A penalty, \(\lambda\), is added to predicted probabilities with ranks greater that some value, \(k\). Everything else is the same as APS.

        • Not sure what Split is, but Cross-Conformal is CV applied to LAC and APS.

    • {{SelfCalibratingConformal}} (Paper) - Combines Venn-Abers calibration and conformal prediction to deliver calibrated point predictions alongside prediction intervals with finite-sample validity conditional on these predictions.
  • Notes from
  • Resources
  • Papers
  • Normal PIs require iid data while conformal PIs only require the “identically distributed” part (not independent) and therefore should provide more robust coverage.
  • Continuous outcome (link) using quantile regression

Classification

  • LAC (aka Score Method) Process
    1. Split data into Train, Calibration (aka Validation), and Test
    2. Train the model on the training set
    3. On the calibration (aka validation) set, compute the conformity scores only for the observed class (i.e. true label) for each observation
      \[ s_{i, j} = 1 - \hat p_{i,j}(y_i | X_i) \]
      • Variables
        • \(s_{i,j}\): Conformity Score for the ith observation and class \(j\)
        • \(y_i\): Observed Class
        • \(\hat p_{i,j}\): Predicted probability by the model for class \(j\)
        • \(X_i\): Predictors
        • \(i\): Index of the observed data
        • \(j\): Class of the outcome variable
      • Range: [0, 1]
      • In general, Low = good, High = bad
      • In R, the predicted probabilities for statistical models are always for the event (i.e. \(y_i = 1\)) in a binary outcome context, so when the observed class = 0, the score will be \(s_{i,0} = 1-(1- \hat p_{i, 1}(y_i | X_i)) = \hat p_{i, 1}(y_i | X_i)\) which is just the predicted probability.
    4. Order the conformity scores from highest to lowest
    5. Adjust the chosen the \(\alpha\) using a finite sample correction, \(q_{\text{level}} = 1- \frac{ceil((n_{\text{cal}}+1)\alpha)}{n_{\text{cal}}}\) and calculate the quantile.
    6. Calculate the critical value or threshold for the quantile
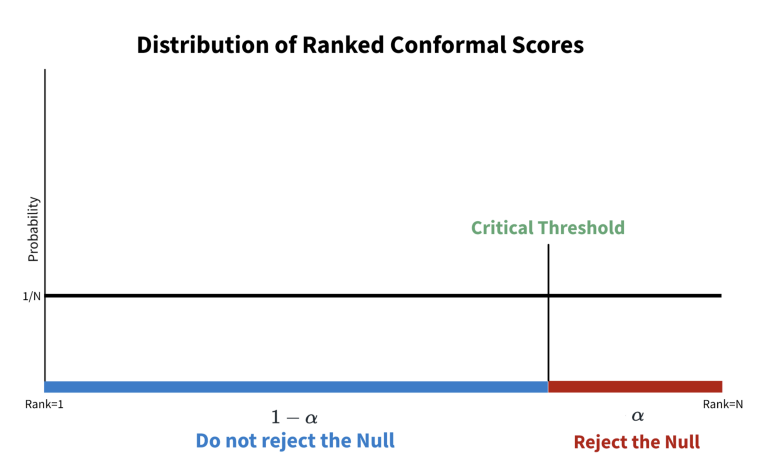
      • x-axis corresponds to an ordered set of conformity scores
      • If \(\alpha = 0.05\), find the score value at the the 95th percentile (e.g. quantile(scores, 0.95))
      • Blue: conformity scores are not statistically significant. They’re within our prediction interval.
      • Red: Very large conformity scores indicate high divergence from the true label. These conformal scores are statistically significant and thereby outside of our prediction interval.
    7. Predict on the Test set and calculate conformity scores for each class
    8. For each test set observation, select classes that have scores below the threshold score as the model prediction.
      • An observation could potentially have both classes or no classes selected. ( Not sure if this is true in a binary outcome situation)
  • Example: LAC Method, Multinomial

    • Model

      classifier = LogisticRegression(random_state=42)
classifier.fit(X_train, y_train)

    • Scores calculated using only the predicted probability for the true class on the Validation set (aka Calibration set)

      # Get predicted probabilities for calibration set
y_pred = classifier.predict(X_Cal)
y_pred_proba = classifier.predict_proba(X_Cal)
si_scores = []
# Loop through all calibration instances
for i, true_class in enumerate(y_cal):
    # Get predicted probability for observed/true class
    predicted_prob = y_pred_proba[i][true_class]
    si_scores.append(1 - predicted_prob)

    • The threshold determines what coverage our predicted labels will have

      number_of_samples = len(X_Cal)
alpha = 0.05
qlevel = (1 - alpha) * ((number_of_samples + 1) / number_of_samples)
threshold = np.percentile(si_scores, qlevel*100)
print(f'Threshold: {threshold:0.3f}')
#> Threshold: 0.598
      • Finite sample correction for the 95th quantile: multiply 0.95 by (n+1)/n

    • Threshold is then used to get predicted labels of the test set

      # Get standard predictions for comparison
y_pred = classifier.predict(X_test)
# Calc scores, then only take scores in the 95% conformal PI
prediction_sets = (1 - classifier.predict_proba(X_test) <= threshold)

# Get labels for predictions in conformal PI
def get_prediction_set_labels(prediction_set, class_labels):
    # Get set of class labels for each instance in prediction sets
    prediction_set_labels = [
        set([class_labels[i] for i, x in enumerate(prediction_set) if x]) for prediction_set in 
        prediction_sets]
    return prediction_set_labels

# Compare conformal prediction with observed and traditional preds
results_sets = pd.DataFrame()
results_sets['observed'] = [class_labels[i] for i in y_test]
results_sets['conformal'] = get_prediction_set_labels(prediction_sets, class_labels)
results_sets['traditional'] = [class_labels[i] for i in y_pred]
results_sets.head(10)
#>    observed  conformal        traditional
#> 0  blue      {blue}           blue
#> 1  green     {green}          green
#> 2  blue      {blue}           blue
#> 3  green     {green}          green
#> 4  orange    {orange}         orange
#> 5  orange    {orange}         orange
#> 6  orange    {orange}         orange
#> 7  orange    {blue, orange}   blue
#> 8  orange    {orange}         orange
#> 9  orange    {orange}         orange
      • conformity scores are calculated for each potential class using the predicted probabilities on the test set
      • The predicted class for an observation is determined by whether a class has a score below the threshold.
      • Therefore, an observation may have 1 or more predicted classes or 0 predicted classes.

    • Statistics (See Statistics section for functions)

      • Overall

        weighted_coverage = get_weighted_coverage(
    results['Coverage'], results['Class counts'])

weighted_set_size = get_weighted_set_size(
    results['Average set size'], results['Class counts'])

print (f'Overall coverage: {weighted_coverage}')
print (f'Average set size: {weighted_set_size}')
#> Overall coverage: 0.947
#> Average set size: 1.035
        • Overall coverage is very close to the target coverage of 95%, therefore, marginal coverage is achieved which is expected for this method

      • Per Class

        results = pd.DataFrame(index=class_labels)
results['Class counts'] = get_class_counts(y_test)
results['Coverage'] = get_coverage_by_class(prediction_sets, y_test)
results['Average set size'] = get_average_set_size(prediction_sets, y_test)
results
#>         Class counts  Coverage   Average set size
#> blue    241           0.817427   1.087137
#> orange  848           0.954009   1.037736
#> green   828           0.977053   1.016908
        • Overall coverage (i.e. for all labels) will be at or very near 95% but coverage for individual classes may vary.
          • An illustration of how this method lacks Conditional Coverage
          • Solution: Get thresholds for each class. (See next example)
        • Note that the blue class had substantially fewer observations that the other 2 classes.
  • Example: LAC-adapted - Threshold per Class

    • Don’t think {{mapie}} has this option.

    • Also possible do this for subgroups of data, such as ensuring equal coverage for a diagnostic across racial groups, if we found coverage using a shared threshold led to problems.

    • Calculate individual class thresholds

      # Set alpha (1 - coverage)
alpha = 0.05
thresholds = []
# Get predicted probabilities for calibration set
y_cal_prob = classifier.predict_proba(X_Cal)
# Get 95th percentile score for each class's s-scores
for class_label in range(n_classes):
    mask = y_cal == class_label
    y_cal_prob_class = y_cal_prob[mask][:, class_label]
    s_scores = 1 - y_cal_prob_class
    q = (1 - alpha) * 100
    class_size = mask.sum()
    correction = (class_size + 1) / class_size
    q *= correction
    threshold = np.percentile(s_scores, q)
    thresholds.append(threshold)

    • Apply individual class thresholds to test set scores

      # Get Si scores for test set
predicted_proba = classifier.predict_proba(X_test)
si_scores = 1 - predicted_proba

# For each class, check whether each instance is below the threshold
prediction_sets = []
for i in range(n_classes):
    prediction_sets.append(si_scores[:, i] <= thresholds[i])
prediction_sets = np.array(prediction_sets).T

# Get prediction set labels and show first 10
prediction_set_labels = get_prediction_set_labels(prediction_sets, class_labels)

    • Statistics

      • Overall

        weighted_coverage = get_weighted_coverage(
    results['Coverage'], results['Class counts'])

weighted_set_size = get_weighted_set_size(
    results['Average set size'], results['Class counts'])

print (f'Overall coverage: {weighted_coverage}')
print (f'Average set size: {weighted_set_size}')
#> Overall coverage: 0.95
#> Average set size: 1.093
        • Similar to previous example

      • Per Class

        results = pd.DataFrame(index=class_labels)
results['Class counts'] = get_class_counts(y_test)
results['Coverage'] = get_coverage_by_class(prediction_sets, y_test)
results['Average set size'] = get_average_set_size(prediction_sets, y_test)
results
#>         Class counts  Coverage   Average set size
#> blue    241           0.954357   1.228216
#> orange  848           0.956368   1.139151
#> green   828           0.942029   1.006039
        • Coverages now very close to 95% and the average set sizes have increased, especially for Blue.

Continuous

  • Conformalized Quantile Regression Process

    1. Split data into Training, Calibration, and Test sets
      • Training data: data on which the quantile regression model learns.
      • Calibration data: data on which CQR calibrates the intervals.
        • In the example, he split the data into 3 equal sets
      • Test data: data on which we evaluate the goodness of intervals.
    2. Fit quantile regression model on training data.
    3. Use the model obtained at previous step to predict intervals on calibration data.
      • PIs are predictions at the quantiles:
        • (alpha/2)*100) (e.g 0.025, alpha = 0. 05)
        • (1-(alpha/2))*100) (e.g. 0.975)
    4. Compute conformity scores on calibration data and intervals obtained at the previous step.
      • Residuals are calculated for the PI vectors
      • Scores are calculated by taking the row-wise maximum of both (upper/lower quantile) residual vectors (e.g s_i <- pmax(lower_pi_res, upper_pi_res))
    5. Get 1-alpha quantile from the distribution of conformity scores (e.g threshold <- quantile(s_i, 0.95)
      • This score value will be the threshold
    6. Use the model obtained at step 1 to make predictions on test data.
      • Compute PI vectors (i.e. predictions at the previously stated quantiles) on Test set
      • i.e. Same calculation as with the calibration data in step 2 where you use the model to predict at upper and lower PI quantiles.
    7. Compute lower/upper end of the interval by subtracting/adding the threshold from/to the quantile predictions (aka PIs)
      • Lower conformity interval: lower_pi <- test_lower_pred - threshold
      • Upper conformity interval: upper_pi <- test_upper_pred + threshold

  • Example: Quantile Random Forest

    import numpy as np
from skgarden import RandomForestQuantileRegressor

alpha = .05

# 1. Fit quantile regression model on training data
model = RandomForestQuantileRegressor().fit(X_train, y_train)

# 2. Make prediction on calibration data
y_cal_interval_pred = np.column_stack([
    model.predict(X_cal, quantile=(alpha/2)*100), 
    model.predict(X_cal, quantile=(1-alpha/2)*100)])

# 3. Compute conformity scores on calibration data
y_cal_conformity_scores = np.maximum(
    y_cal_interval_pred[:,0] - y_cal, 
    y_cal - y_cal_interval_pred[:,1])

# 4. Threshold: Get 1-alpha quantile from the distribution of conformity scores
#    Note: this is a single number
quantile_conformity_scores = np.quantile(
    y_cal_conformity_scores, 1-alpha)

# 5. Make prediction on test data
y_test_interval_pred = np.column_stack([
    model.predict(X_test, quantile=(alpha/2)*100), 
    model.predict(X_test, quantile=(1-alpha/2)*100)])

# 6. Compute left (right) end of the interval by
#    subtracting (adding) the quantile to the predictions
y_test_interval_pred_cqr = np.column_stack([
    y_test_interval_pred[:,0] - quantile_conformity_scores,
    y_test_interval_pred[:,1] + quantile_conformity_scores])

Statistics

  • Average Set Size

    • The average number of predicted classes per observation since there can be more than 1 predicted class in the conformal PI

    • Example:

      # average set size for each class
def get_average_set_size(prediction_sets, y_test):
    average_set_size = []
    for i in range(n_classes):
        average_set_size.append(
            np.mean(np.sum(prediction_sets[y_test == i], axis=1)))
    return average_set_size   

# Overall average set size (weighted by class size)
# Get class counts
def get_class_counts(y_test):
    class_counts = []
    for i in range(n_classes):
        class_counts.append(np.sum(y_test == i))
    return class_counts

def get_weighted_set_size(set_size, class_counts):
    total_counts = np.sum(class_counts)
    weighted_set_size = np.sum((set_size * class_counts) / total_counts)
    weighted_set_size = round(weighted_set_size, 3)
    return weighted_set_size
  • Coverage

    • Classification: Percentage of correct classifications

    • Example: Classification

      # coverage for each class
def get_coverage_by_class(prediction_sets, y_test):
    coverage = []
    for i in range(n_classes):
        coverage.append(np.mean(prediction_sets[y_test == i, i]))
    return coverage

# overall coverage (weighted by class size)
# Get class counts
def get_class_counts(y_test):
    class_counts = []
    for i in range(n_classes):
        class_counts.append(np.sum(y_test == i))
    return class_counts

def get_weighted_coverage(coverage, class_counts):
    total_counts = np.sum(class_counts)
    weighted_coverage = np.sum((coverage * class_counts) / total_counts)
    weighted_coverage = round(weighted_coverage, 3)
    return weighted_coverage

Visualization

  • Confusion Matrix
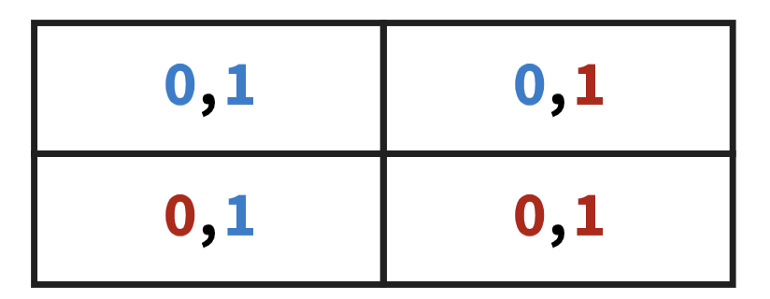
    • Binary target where labels are 0 and 1
    • Interpretation
      • Top-left: predictions where both labels are not statistically significant (i.e. inside the “prediction interval”).
        • The model predicts both classes well since both labels have low scores.
        • Depending the threshold, maybe the model could be relatively agnostic (e.g. predicted probabilites like 0.50-0.50, 0.60-0.40)
      • Bottom-right: predictions where both labels are statistically significant  (i.e. outside the “prediction interval”).
        • Model totally whiffs. Confident it’s one label when it’s actually another.
          • Example
            • 1 (truth) - low predicted probability = high score -> Red and significant
            • 0 - high predicted probability = high score -> Red and significant
      • Top-right: predictions where all 0 labels are not statistically significant.
        • Model predicted the 0=class well (i.e. low scores) but the 1-class poorly (i.e. high scores)
      • Bottom-left: predictions where all 1 labels are not statistically significant. Here, the model predicted that 1 is the true class.
        • Vice versa of top-right