GLMM

Misc

Packages
- {glmmTMB}
  - Beta, Beta-Binomial, Beta-Ordinal, various extensions for Negative Binomial and Poisson, Log-Normal, Tweedie, Student-T, Gamma, Zero-Inflated, Truncated (See Manual >> nbinom2 for details)
  - Currently has an experimental implementation of fixed effect priors which can be a solution to complete separation errors, singular fits, and instability (Link).
  - Supports parallelization through OpenMP but might not be supported by Mac and has significant overhead on Windows.
- {GLMMadaptive} - For binary/dichotomous data and count data with small counts and few repeated measurements, the accuracy of Laplace approximations (i.e. {glmmTMB}) is low. This package uses adaptive Gaussian quadrature rule which is the recommended, albeit more computationally intensive, approximation method for MLE in this situation.
  - Supported Distribution Families: Student’s-t, Beta, Zero-Inflated and Hurdle Poisson and Negative Binomial, Hurdle Log-Normal, Hurdle Beta, Gamma, and Censored Normal
  - Currently no nested or crossed random effects designs
  - Can penalize fixed effects with a student-t prior
  - Parallelization through {optimParallel} which doesn’t seem to have any OS limitations.
- {glmmPen} (Vignette)
  - Fits high dimensional penalized generalized linear mixed models using the Monte Carlo Expectation Conditional Minimization (MCECM) algorithm.
  - Performs variable selection on both the fixed and random effects simultaneously through MCP, SCAD, or LASSO penalties.
  - Supports Binomial, Gaussian, and Poisson data with canonical links
- {mgcv::gamm} - Fits the specified generalized additive mixed model (GAMM) to data, by a call to {nlme::lme} in the normal errors identity link case, or by a call to gammPQL (a modification of glmmPQL from {MASS}) otherwise.
  - ** There is a bug (as of Jan 2025) in gamm that prohibits the random effects from being included in the fitted values when the random argument is used and there’s not a spline in the formula ** (See Examples >> Example 1)
    - In docs for the function, it does say that a manual calculation is required, but I’ve only found that to be the case in the specification stated above.
  - Performs poorly with binary data, since it uses PQL. It is better to use gam with s(...,bs="re") terms, or {gamm4}.
  - Usually much slower than gam
  - Correlation Structures: The routine will be very slow and memory intensive if correlation structures are used for the very large groups of data.
    - e.g. Attempting to run the spatial example in the examples section with many 1000’s of data is definitely not recommended: often the correlations should only apply within clusters that can be defined by a grouping factor, and provided these clusters do not get too huge then fitting is usually possible.
- {gamm4} - Generalized Additive Mixed Models using {mgcv} and {lme4}
  - Based on gamm from mgcv, but uses lme4 rather than nlme as the underlying fitting engine
  - More robust numerically than gamm, and by avoiding PQL gives better performance for binary and low mean count data.
  - Most useful when:
    - The random effects are not i.i.d.
    - There are large numbers of random coeffecients (more than several hundred), each applying to only a small proportion of the response data.
  - Tensor product smoothing is available via t2 terms
  - Issues
    - It can not handle most multi-penalty smooths (i.e. not te type tensor products or adaptive smooths)
    - No facilty for nlme style correlation structures.
    - For fitting GAMMs with modest numbers of i.i.d. random coefficients then gamm4 is slower than gam (or bam for large data sets)
Papers
- High performance implementation of the hierarchical likelihood for generalized linear mixed models: an application to estimate the potassium reference range in massive (codelectronic health records datasets
  - A high-performance, direct implementation of the hierarchical-likelihood for GLMMs in the R package TMB
  - The hierarchical likelihood approach to GLMMs is a methodologically rigorous framework for the estimation of GLMMs that is based on the Laplace Approximation (LA), which replaces integration with numerical optimization, and thus scales very well with dimensionality.
  - Code (+ parallelization option)
    - SingleRE: Analyzes a Poisson GLM with a single random effect
    - MultipleRE: Analyzes a Poisson GLM with multiple random effects

Model Equation

Equation
\[ g\{E(y_i \mid b_i)\} = \beta X_i + b_i Z_i, \]
- \(g(⋅)\): A monotonic link function
- \(X_i\): A design matrix for the fixed effects
- \(\beta\): Fixed effects coefficients
- \(Z_i\): A design matrix for the random effects that’s assumed to be a subset of \(X_i\)
- \(b_i\): Random effects coefficients

Examples

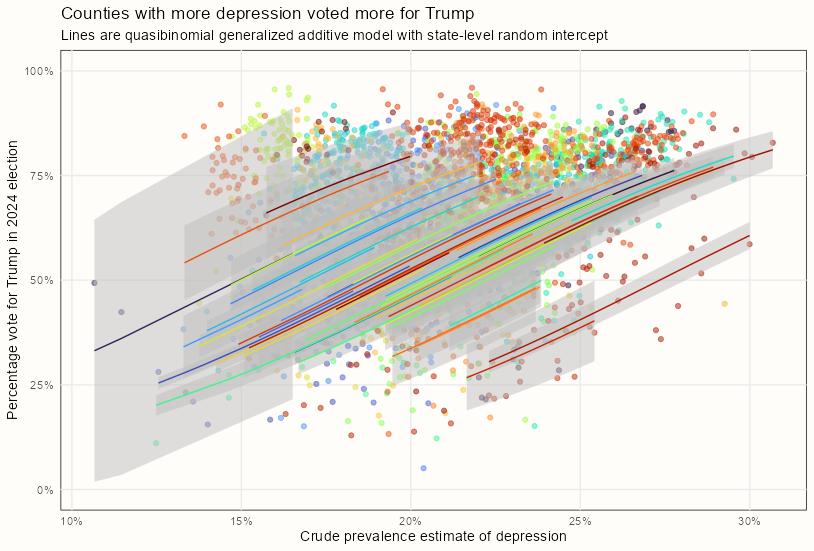
Example 1: GAMM with Varying Intercepts (source, source)

Did counties with more depressed people voted more for Trump?
Binomial and Quasi-Binomial distributions are used to model a percent response variable

library(tidyverse)

# https://stacks.cdc.gov/view/cdc/129404
dep <- readxl::read_excel("cdc_129404_DS1.xlsx", skip = 1)
election_data_url <- "https://raw.githubusercontent.com/tonmcg/US_County_Level_Election_Results_08-24/refs/heads/master/2024_US_County_Level_Presidential_Results.csv"
votes <- read_csv(election_data_url)

dat_votes_dep <- votes |>
  inner_join(dep, by = c("county_fips" = "CountyFIPS code")) |>
  mutate(cpe = `Crude Prevalence Estimate` / 100,
         aape = `Age-adjusted Prevalence Estimate` / 100)
glimpse(votes_dep_dat)
#> Rows: 3,107
#> Columns: 18
#> $ state_name                                           <chr> "Alabama", "Alabama", "Alabama", "Alabama", "Alabama", "Alabama", "Alaba…
#> $ county_fips                                          <chr> "01001", "01003", "01005", "01007", "01009", "01011", "01013", "01015", …
#> $ county_name                                          <chr> "Autauga County", "Baldwin County", "Barbour County", "Bibb County", "Bl…
#> $ votes_gop                                            <dbl> 20447, 95144, 5578, 7563, 25271, 1099, 5167, 34841, 8704, 11342, 16901, …
#> $ votes_dem                                            <dbl> 7429, 24763, 4120, 1617, 2569, 2983, 3248, 13170, 5402, 1550, 2697, 2511…
#> $ total_votes                                          <dbl> 28139, 120973, 9766, 9230, 28024, 4104, 8459, 48435, 14215, 12965, 19708…
#> $ diff                                                 <dbl> 13018, 70381, 1458, 5946, 22702, -1884, 1919, 21671, 3302, 9792, 14204, …
#> $ per_gop                                              <dbl> 0.7266427, 0.7864895, 0.5711653, 0.8193933, 0.9017628, 0.2677875, 0.6108…
#> $ per_dem                                              <dbl> 0.26401080, 0.20469857, 0.42187180, 0.17518960, 0.09167142, 0.72685185, …
#> $ per_point_diff                                       <dbl> 0.46263193, 0.58179098, 0.14929347, 0.64420368, 0.81009135, -0.45906433,…
#> $ CountyName                                           <chr> "Autauga", "Baldwin", "Barbour", "Bibb", "Blount", "Bullock", "Butler", …
#> $ `State Name`                                         <chr> "Alabama", "Alabama", "Alabama", "Alabama", "Alabama", "Alabama", "Alaba…
#> $ `Crude Prevalence Estimate`                          <dbl> 24.52297, 24.61480, 23.68052, 24.80906, 26.65236, 22.00814, 23.88319, 26…
#> $ `95% Confidence Interval for Crude Estimates`        <chr> "23.3-25.8", "23.3-26", "22.7-24.8", "23.6-26.1", "25.3-28.1", "21-23.1"…
#> $ `Age-adjusted Prevalence Estimate`                   <dbl> 24.9, 25.7, 24.2, 25.1, 27.5, 22.4, 24.9, 27.0, 24.9, 27.5, 27.6, 25.3, …
#> $ `95% Confidence Interval for Age-adjusted Estimates` <chr> "23.6-26.4", "24.3-27.1", "23.1-25.3", "23.9-26.4", "26-29", "21.3-23.6"…
#> $ cpe                                                  <dbl> 0.2452297, 0.2461480, 0.2368052, 0.2480906, 0.2665236, 0.2200814, 0.2388…
#> $ aape                                                 <dbl> 0.249, 0.257, 0.242, 0.251, 0.275, 0.224, 0.249, 0.270, 0.249, 0.275, 0.…

per_gop: Percentage of votes cast for the Republican presidential candidate
cpe: Crude Prevalence Estimate (percentage); depression measure

mod_bin_inter <- 
  lme4::glmer(per_gop ~ cpe + (1 | state_name), 
              family = "binomial", 
              weights = total_votes,
              data = dat_votes_dep)

summary(mod_bin_inter)
#> Random effects:
#>  Groups     Name        Variance Std.Dev.
#>  state_name (Intercept) 0.4636   0.6809  
#> Number of obs: 3107, groups:  state_name, 50
#> 
#> Fixed effects:
#>             Estimate Std. Error z value Pr(>|z|)    
#> (Intercept) -3.27338    0.09572   -34.2   <2e-16 ***
#> cpe         16.40275    0.01073  1529.1   <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Correlation of Fixed Effects:
#>     (Intr)
#> cpe -0.022

This lets the vote for Trump in any state vary for all the state-specific things that aren’t in our model.
States weighted based on their overall number of voters, which makes particular sense for a binomial or similar family response.
{lme4} doesn’t support a quasi-binomial distribution. With the binomial distribution, it’s assumed that the relationship between the mean and variance is \(p(1-p)/n\) which means overdispersion isn’t being handled correctly.
- This results in CIs that are too narrow.
We see an overall (constant nation-wide) relationship (fixed effect) between depression (cpe) and voting (per_gop) in the counties (observation-level) within each state.

# must be a factor to use as a random effect in gam
dat_votes_dep <- mutate(dat_votes_dep, 
                        state_name = as.factor(state_name))

# These two specifications included random effects in fitted values 
mod_quasi_bin_inter_gam <- 
  mgcv::gam(per_gop ~ cpe + s(state_name, bs = 're'),
            weights = total_votes, 
            family = quasibinomial, 
            data = dat_votes_dep)

mod_quasi_bin_inter_spl <- 
  mgcv::gamm(per_gop ~ cpe + s(state_name, bs = 're'),
             weights = total_votes, 
             family = quasibinomial, 
             data = dat_votes_dep)

# This specification does NOT include randome effects in fitted values
# mod_quasi_bin_inter_lme <- 
#   mgcv::gamm(per_gop ~ cpe,
#              random = list(state_name = ~ 1),
#              weights = total_votes, 
#              family = quasibinomial, 
#              data = dat_votes_dep)

summary(mod_quasi_bin_inter_spl$gam)
#> Parametric coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  -3.1087     0.1392  -22.33   <2e-16 ***
#> cpe          15.7091     0.5869   26.77   <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Approximate significance of smooth terms:
#>                 edf Ref.df     F p-value    
#> s(state_name) 45.65     49 20.99  <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> R-sq.(adj) =  0.346   
#>   Scale est. = 3193.2    n = 3107

broom::glance(mod_quasi_bin_inter_gam)
#> # A tibble: 1 × 9
#>      df logLik   AIC   BIC  deviance df.residual  nobs adj.r.squared  npar
#>   <dbl>  <dbl> <dbl> <dbl>     <dbl>       <dbl> <int>         <dbl> <int>
#> 1  50.4     NA    NA    NA 10024845.       3057.  3107         0.345    52

{mgcv} does have a quasi-binomial family available
Either the gam function or the gamm function can be used to fit this model by using s(state_name, bs = "re"). It should NOT be fit using gamm and the random argument, unless you aren’t interested the fitted values or you want to include the random effects manually.
- Using the California data as my test case, I also noticed that using gamm without a spline produced negative fitted values which I don’t think should be possible with a Quasi-Binomial.
gamm vs. gam (with spline “re” specification)
- Even though there are differences, these are practically the same model
- There are fewer effective degrees of freedom (edf) used to fit the spline (i.e. smoother curve) using gamm than with gam (45.65 vs 48.44).
- The effect size is slightly lower using gamm vs gam (15.7091 vs 16.3333)
- The standard error is slightly lower using gamm vs gam (0.5869 vs 0.6224)
- According to the docs, gam should be the faster fitting function
The standard error for cpe is much higher 0.5869, compared to 0.0107 in the Binomial model
- This will result in fatter, more realistic CI intervals

Visualization

Code

# using gam
aug_quasi_bin_inter_gam <- 
  broom::augment(mod_quasi_bin_inter, 
                 type.predict = "response") |> 
  mutate(lower = .fitted - 1.96 * .se.fit,
         upper = .fitted + 1.96 * .se.fit)

# using gamm
pred_quasi_bin_inter_spl <- 
  predict(mod_quasi_bin_inter_spl$gam, 
          se.fit = TRUE, 
          type = "response")
aug_quasi_bin_inter_spl <- 
  dat_votes_dep |>
  mutate(.fitted = pred_quasi_bin_inter_spl$fit,
         lower = .fitted - 1.96 * pred_quasi_bin_inter_spl$se.fit,
         upper = .fitted + 1.96 * pred_quasi_bin_inter_spl$se.fit) |> 
  select(per_gop, cpe, state_name, .fitted, lower, upper)


ggplot(aug_quasi_bin_inter_gam, 
       aes(x = cpe, 
           group = state_name)) +
  geom_point(aes(y = per_gop, 
                 color = state_name), 
             alpha = 0.5) +
  geom_ribbon(aes(ymin = lower, 
                  ymax = upper), 
              fill = "gray", 
              alpha = 0.5) +
  geom_line(aes(y = .fitted, 
                color = state_name)) +
  scale_y_continuous(limits = c(0, 1), 
                     label = scales::label_percent()) +
  scale_x_continuous(label = scales::label_percent()) +
  scale_color_viridis_d(option = "turbo") + 
  labs(x = "Crude prevalence estimate of depression",
       y = "Percentage vote for Trump in 2024 election",
       subtitle = "Lines are quasibinomial generalized additive model with state-level random intercept",
       title = "Counties with more depression voted more for Trump") +
  theme_notebook(legend.position = "none")

mod_quasi_bin_inter_spat_lme <- 
  mgcv::gamm(per_gop ~ cpe + s(long, lat),
             random = list(state_name = ~1), 
             weights = total_votes, 
             family = quasibinomial, 
             data = dat_votes_dep_spat)

summary(mod_quasi_bin_inter_spat_lme)
#> Parametric coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  -2.8878     0.1481  -19.50   <2e-16 ***
#> cpe          15.0166     0.6271   23.95   <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Approximate significance of smooth terms:
#>               edf Ref.df     F p-value    
#> s(long,lat) 25.41  25.41 7.129  <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> R-sq.(adj) =  0.0981   
#>   Scale est. = 3005.3    n = 3107

AIC(mod_quasi_bin_inter_spat_lme$lme, mod_quasi_bin_inter_spl$lme)
#>                                  df      AIC
#> mod_quasi_bin_inter_spat_lme$lme  7 8806.902
#> mod_quasi_bin_inter_spl$lme       4 8879.840

With a spline function in the formula, there will now be random effects included with the fitted values when using gamm with random argument
- I assume this is a bug.
The hope was to account for some of the probable spatial autorcorrelation. The R² indicates an even worse fit while potentially more predictive given the lower AIC.
- See Mixed Effects, Residual Covariance Structures >> Examples >> Spatial Autocorrelation >> Example 1
Note that the data used in this model is dat_votes_dep_spat which includes the lat and long predictors that represent centroids for each county. Code is included below.

Visualization

Code

pred_quasi_bin_inter_spat_lme <- 
  predict(mod_quasi_bin_inter_spat_lme$gam, 
          se.fit = TRUE, 
          type = "response")

aug_quasi_bin_inter_spat_lme <- 
  dat_votes_dep_spat |>
  mutate(.fitted = pred_quasi_bin_inter_spat_lme$fit,
         lower = .fitted - 1.96 * pred_quasi_bin_inter_spat_lme$se.fit,
         upper = .fitted + 1.96 * pred_quasi_bin_inter_spat_lme$se.fit) |> 
  select(per_gop, cpe, state_name, .fitted, lower, upper)

ggplot(aug_quasi_bin_inter_spat_lme, 
       aes(x = cpe, 
           group = state_name)) +
  geom_point(aes(y = per_gop, 
                 color = state_name), 
             alpha = 0.5) +
  geom_ribbon(aes(ymin = lower, 
                  ymax = upper), 
              fill = "black", 
              alpha = 0.5) +
  scale_y_continuous(limits = c(0, 1), 
                     label = scales::label_percent()) +
  scale_x_continuous(label  = scales::label_percent()) +
  scale_color_viridis_d(option = "turbo") + 
  facet_wrap(~state_name) +
  labs(x = "Crude prevalence estimate of depression",
       y = "Percentage vote for Trump in 2024 election",
       subtitle = "Gray ribbons are 95% confidence intervals from quasibinomial generalized additive model with spatial effect and state-level random intercept effect",
       title = "Counties with more depression voted more for Trump") +
  theme_notebook(legend.position = "none")

A closer look at the black ribbons in these plots will show some states have some really squiggly lines (overfitting). This must be due to the longitude and latitude spline. I attempted to reduce the number on knots, and even at k = 2, some ribbons remained very squiggly. I’m not sure why some of these lines werent’ affected. I didn’t drill down into the individual states data and fitted values further to see what was going on.
Some state’s data and their trend lines (ribbons) didn’t seem to match either.

Centroid Calculations

Code

library(sf)

download.file('https://www2.census.gov/geo/tiger/GENZ2023/shp/cb_2023_us_county_500k.zip',
              destfile = "../../Data/cb_2023_us_county_500k.zip", mode = "wb")

unzip("../../Data/cb_2023_us_county_500k.zip",
      exdir = "../../Data")

counties <- st_read("../../Data/cb_2023_us_county_500k.shp")
county_cent <- 
  counties |>
  st_centroid() 

sc <- st_coordinates(county_cent)

county_cent <- 
  county_cent |>
  mutate(long = sc[, 1],
         lat = sc[, 2],
         # combine the two digit state code with the 3 digit county code:
         county_fips = paste0(STATEFP, COUNTYFP))

dat_votes_dep_spat <- 
  dat_votes_dep |>
  left_join(county_cent, by = "county_fips")

Example 2: GAMM with Varying Intercepts and Varying Slopes (source)

mod_quasi_bin_intslp_spat <- 
  mgcv::gamm(per_gop ~ cpe + s(long, lat),
             random = list(state_name = ~1 + cpe), 
             weights = total_votes, 
             family = quasibinomial, 
             data = dat_votes_dep_spat

summary(mod_quasi_bin_intslp_spat$gam)
#> Parametric coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  -2.0995     0.5203  -4.035 5.59e-05 ***
#> cpe          10.4828     2.5033   4.188 2.90e-05 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Approximate significance of smooth terms:
#>               edf Ref.df     F p-value    
#> s(long,lat) 26.15  26.15 8.248  <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> R-sq.(adj) =  0.186   
#>   Scale est. = 2597.3    n = 3107

AIC(mod_quasi_bin_intslp_spat$lme, mod_quasi_bin_inter_spat_lme$lme)
#>                                  df      AIC
#> mod_quasi_bin_intslp_spat$lme     9 8605.691
#> mod_quasi_bin_inter_spat_lme$lme  7 8806.902

This is a continuation from Example 1 where mod_quasi_bin_inter_spat_lme is a varying intercepts only model
This is an overall better model — better fit (higher R²) and more predictive (lower AIC)
Development of this model continues at Mixed Effects, Residual Covariance Structures >> Examples >> Spatial Autocorrelation >> Example 1
Visualization code can be found in Example 1