Analysis

Misc

  • Also see
  • Boundary Analysis
    • The assessment of whether significant geographic boundaries are present and whether the boundaries of multiple variables are spatially correlated.
    • Notes from BoundaryStats: An R package to calculate boundary overlap statistics
    • Packages
      • {BoundaryStats} - Functions for boundary and boundary overlap statistics
    • Boundaries are areas in which spatially distributed variables (e.g., bird plumage coloration, disease prevalence, annual rainfall) rapidly change over a narrow space.
    • Boundary Statistics
      • The length of the longest boundary
      • The number of cohesive boundaries on the landscape
    • Boundary Overlap Statistics
      • The amount of direct overlap between boundaries in variables \(A\) and \(B\)
      • The mean minimum distance between boundaries in \(A\) and \(B\) (i.e. minimums are measured within \(A\))
        • For instance, the minimum distance between \(\text{boundary}_{A,i}\) and \(\text{boundary}_{A,j}\)
      • The mean minimum distance from boundaries in \(A\) to boundaries in \(B\)
    • Use Cases
      • By identifying significant cohesive boundaries, researchers can delineate relevant geographic sampling units (e.g., populations as conservation units for a species or human communities with increased disease risk).
      • Associations between the spatial boundaries of two variables can be useful in assessing the extent to which an underlying landscape variable drives the spatial distribution of a dependent variable.
      • Identifying neighborhood effects on public health outcomes, including COVID-19 infection risk or spatial relationships between high pollutant density and increased disease risk.

Terms

  • Areal (aka Lattice) Data - Data in a study region that is partitioned into a limited number of areas, with outcomes being aggregated or summarized within those areas (instead of at points). Examples include:
    • Population density
    • Disease rates
    • Income levels
    • Crime statistics
    • Educational attainment
    • Unemployment rates
  • Buffer - a zone around a geographic feature containing locations that are within a specified distance of that feature, the buffer zone. A buffer is likely the most commonly used tool within the proximity analysis methods. Buffers are usually used to delineate protected zones around features or to show areas of influence.
  • Catchment - The area inside any given polygon is closer to that polygon’s point than any other. Refers to the area of influence from which a retail location, such as a shopping center, or service, such as a hospital, is likely to draw its customers. (also see Retail >> Catchment)
  • Spatial Functional Data - Data comprising curves or functions that are recorded at each spatial location.

Proximity Analysis

  • Example: Basic Workflow

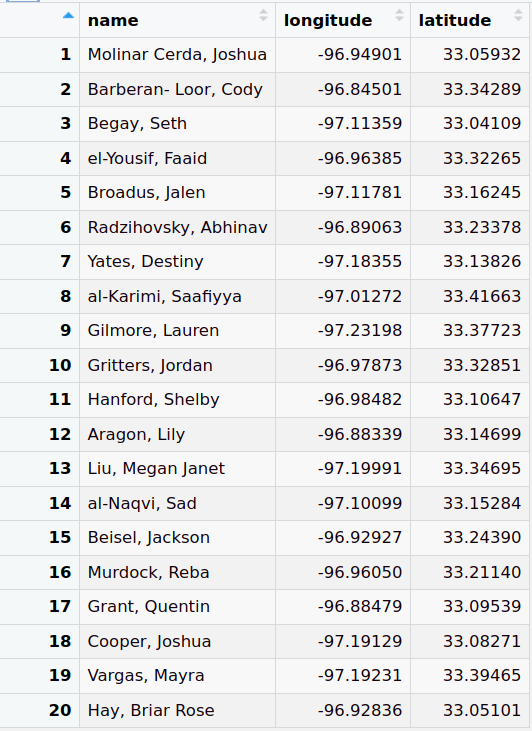
    • Data: Labels, Latitude, and Longitude

    • Create Simple Features (sf) Object

      customer_sf <- 
  customer_table %>%
    sf::st_as_sf(coords = c("longitude", "latitude"),
                 crs = 4326)
      • Merges the longitude and latitude columns into a geometry column and transforms the coordinates in that column according to projection (e.g. crs = 4326)

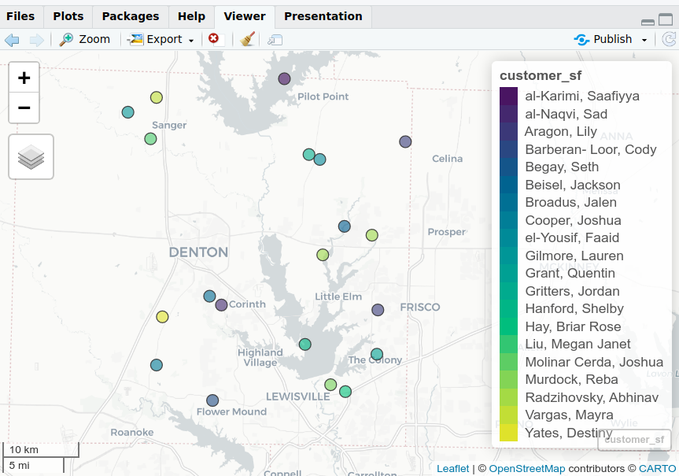
    • View points on a map

      mapview::mapview(customer_sf)

    • Create Buffer Zones

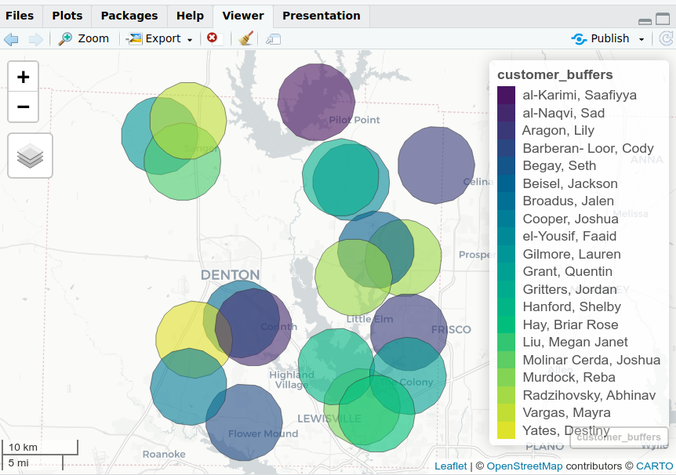
      customer_buffers <- 
  customer_sf %>%
    sf::st_transform(26914) %>%
    sf::st_buffer(5000)

mapview::mapview(customer_buffers)
      • Most of projections use meters, and based on the size of the circles as related to the size of Denton, TX, I’m guessing the radius of each circle is 5000m. Although, that still looks a little small.

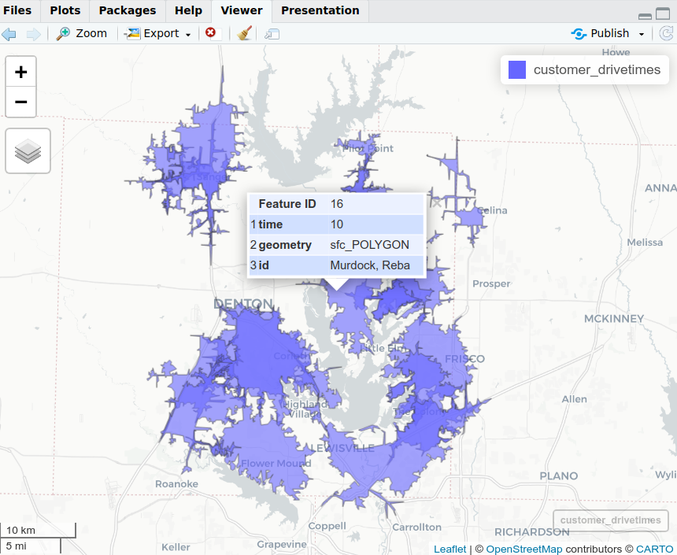
    • Create Isochrones

      customer_drivetimes <- 
  customer_sf %>%
    mapboxapi::mb_isochrone(time = 10, 
                            profile = "driving", 
                            id_column = "name")

mapview::mapview(customer_drivetimes)
      • 10 minutes drive-time from each location
      • time (minutes): The maximum time supported is 60 minutes. Reflects traffic conditions for the date and time at which the function is called.
        • If reproducibility of isochrones is required, supply an argument to the depart_at argument.
      • depart_at: Specifying a time makes it a time-aware isochrone. Useful for modeling peak business hours or rush hour traffic, etc.
        • e.g. Adding depart_at = “2024-01-27T17:30” to the isochrone above gives you a 10-minute driving isochrone with predicted traffic at 5:30pm tomorrow

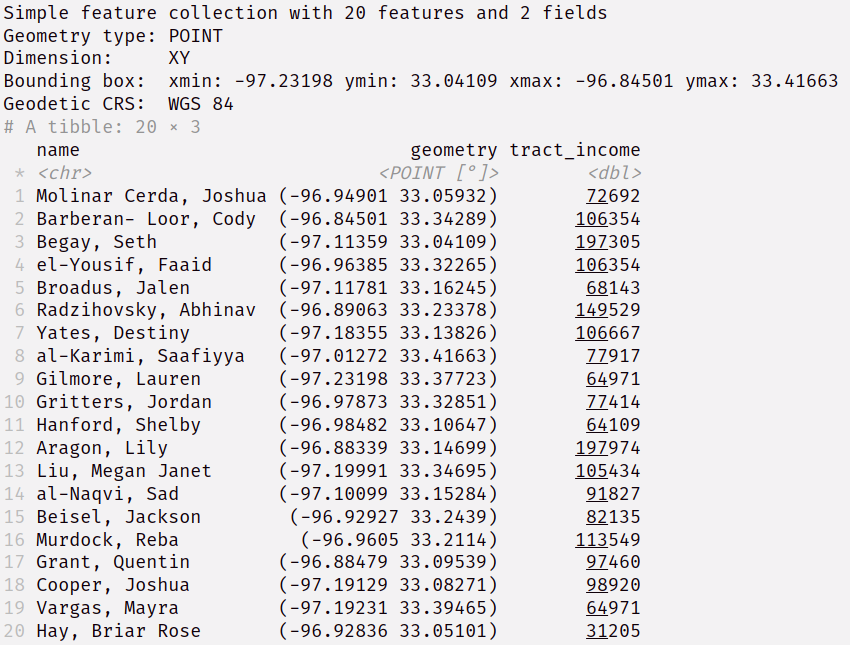
    • Add Demographic Data

      denton_income <- 
  tidycensus::get_acs(
    geography = "tract",
    variables = "B19013_001",
    state = "TX",
    county = "Denton",
    geometry = TRUE
  ) %>%
    select(tract_income = estimate) %>%
    sf::st_transform(st_crs(customer_sf))

customers_with_income <- customer_sf %>%
  sf::st_join(denton_income)

customers_with_income

      • Adds median income estimate according to the census tract each person lives in.

      • Joins on the geometry variable

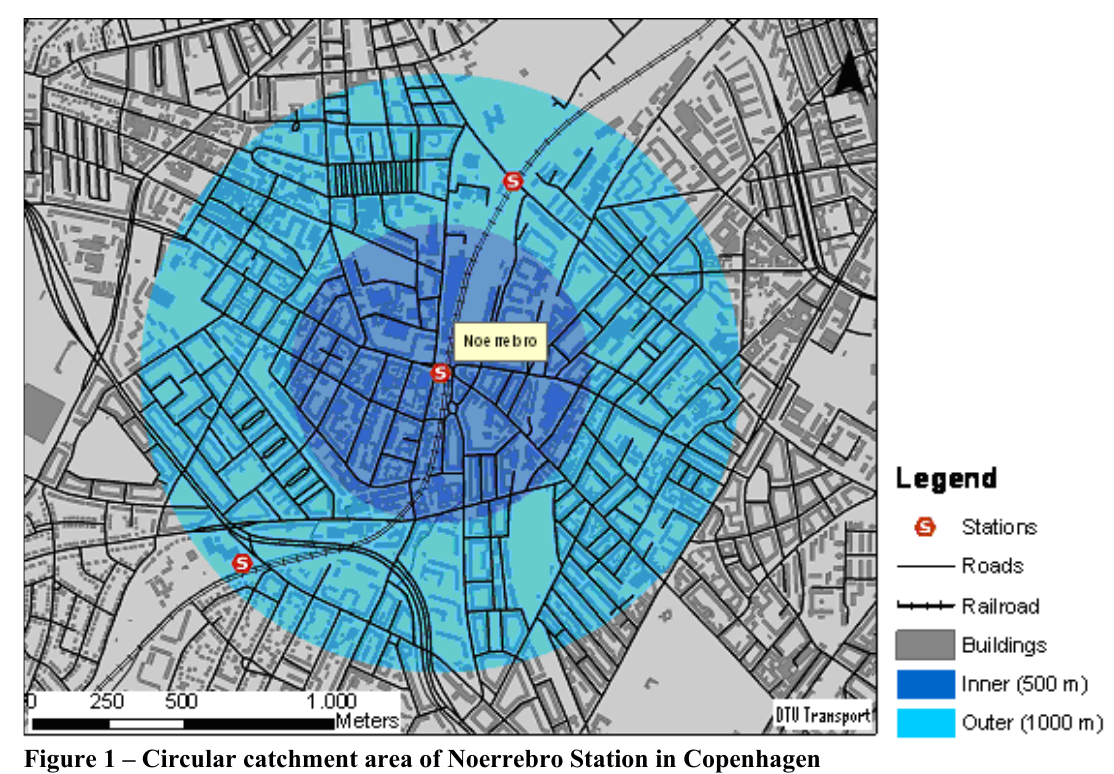
  • Circular Buffer Approach
    • Notes from GIS-based Approaches to Catchment Area Analyses of Mass Transit
    • The simplest and most common used approach to make catchment areas of a location is to consider the Euclidean distance from the location.
    • Due to limitations (See below), it’s best suited for overall analyses of catchment areas.
    • Often the level of detail in the method has been increased by dividing the catchment area into different rings depending on the distance to the station.
      • Example: By applying weights for each ring it is possible to take into account that the expected share of potential travelers at a train station will drop when the distance to the stop is increased.

    • Limitation: Does not take the geographical surroundings into account.
      • Example: In most cases, the actual walking distance to/from a location is longer than the Euclidean distance since there are natural barriers like rivers, buildings, rail tracks etc.
        • This limitation is often coped with by applying a detour factor that reduces the buffer distance to compensate for the longer walking distance.
        • However, in cases where the length of the detours varies considerably within the location’s surroundings, this solution is not very precise.
        • Furthermore, areas that are separated completely from a location, e.g. by rivers, might still be considered as part of the location’s catchment area
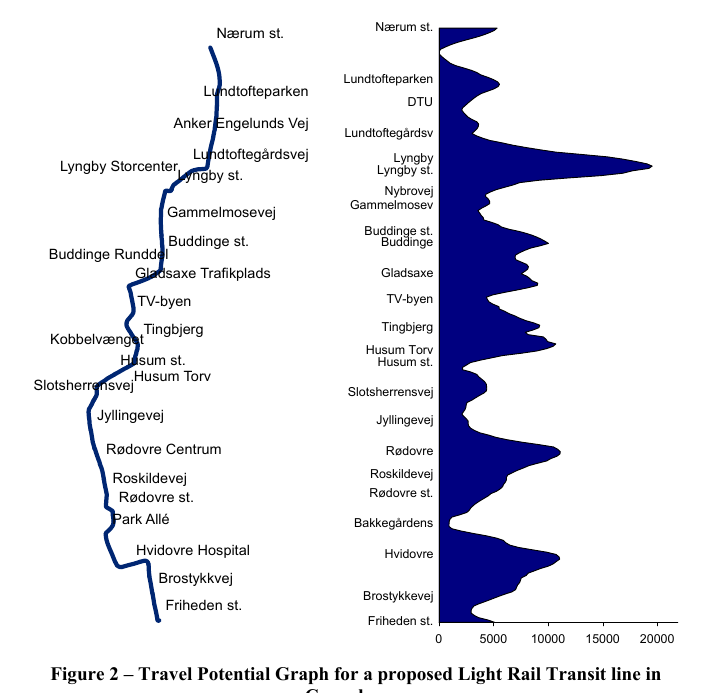
    • Use Case: Ascertain Travel Potential to Determine Potential Station Locations

      • Every 50m along the proposed transit line, calculate the travel potential for that buffer area

        • Using the travel demand data for that buffer area, calculate travel potential

      • Travel Potential Graph

        • Left side represents the transit line.
        • Right Side
          • Y-Axis are locations where buffer areas were created.
          • X-Axis: Travel Potential
            • Not sure if that is just smoothed line with a point estimate of Travel Potential at each location or how exactly those values are calculated.
              • 50m isn’t a large distance so maybe all the locations aren’t shown on the Y-Axis and the number of calculations produces an already, mostly, smooth line on it’s own.
            • Partitioning a buffer zone into rings or some kind of interpolation could provided more granular estimates around the central buffer location.

Spatial Weights

Misc

  • Notes from {spdep} vignettes and its docs.
  • Packages
    • {spdep} - Spatial Dependence: Weighting Schemes, Statistics
  • Workflows
    • Possibly include plotting differences to compare neighbor algorithms to see which best aligns with analysis goals, and testing symmetry and disjointedness of the results. (See Diagnostics, Geospatial)
    • Graph-based
      • Create a points list object (e.g. st_centroid) \(\rightarrow\) Fit neighbors algorithm (e.g. gabrielneigh) \(\rightarrow\) Convert to neighbors list (e.g. graph2nb) \(\rightarrow\) Add spatial weights (e.g. nb2listw)
    • Distance-based
      • Create a points list object (e.g. st_centroid) \(\rightarrow\) If necessary, convert to geographical coordinates (via st_transform) \(\rightarrow\) Fit neighbors algorithm (e.g. knearneigh) \(\rightarrow\) Convert to neighbors list (e.g. knn2nb) \(\rightarrow\) Add spatial weights (e.g. nb2listw)
        • If you only have latitude and longitude columns, you need to convert to a sf object via st_as_sf before creating a points list object (See Geospatial, Preprocessing >> Projections >> Geographic Coordinates)
        • The conversion to geographical coordinates isn’t necessary, but Great Circle distances are more accurate than planar distances.
    • Polygon-based (aka Contiguity-based)
      • Make sure you have sf object or list of SpatialPolygon objects \(\rightarrow\) Create neighbors list via poly2nb \(\rightarrow\) Add spatial weights (e.g. nb2listw)
  • Plot differences between neighbor algorithms

    • It can be difficult to compare algorithms, so this helps make the differences more discernable.

    • Example: From Example: SOI and GG

      # diffnb doesn't handle directed graphs
NY85_nb_gg <- 
  graph2nb(gabrielneigh(coords = NY8_ct_sf),
           sym = TRUE)

diffs <- diffnb(NY85_nb_soi, NY85_nb_gg)

plot(st_geometry(NY8_sf), 
     border = "gray", 
     reset = FALSE,
     main = "Differences between GG (black) and SOI (red)")
plot(NY85_nb_gg, 
     coords = coords_ct, 
     add = TRUE)
plot(diffs, 
     coords = coords_ct, 
     add = TRUE, 
     col = "red", 
     lty = 2)
      • lty = 2 is for dashed lines, yet there are solid red lines in the plot. A solid line indicates a symmetrical link. It happens because dashed lines are drawn from i to j and j to i. This overlap sometimes creates a solid line. (source)
        • Bivand said “sometimes,” so perhaps this isn’t a sure-fire representation of all the symmetric links.
      • There appears to be black dashed lines overlapped with red dashed lines. The black dashed lines are just imperfections in the rendering of the solid black lines. Maybe it’s the angle that igraph or base R has trouble with, but anyways these instances should be interpreted as solid black lines.
  • The all.equal function (docs, from {terra}) can be used to examine the differences in distance calculations

Neighbors Lists

  • Just about everything gets converted to a neighbor list of some sort at the end (e.g. adding spatial weights, moran’s test, plotting)
  • edit can be used to interactively add links (e.g. not detected erroneously) or remove links (e.g. mountain range separates boundaries).
  • Types of Neighbor Lists
    • cell2nb - Takes regular, flat, square grids (via ncols, nrows) as inputs
      • type = rook (default)(shared edge) or queen (shared edge or vertex)
      • torus = TRUE: The grid is mapped onto a torus, removing edge effects.
    • graph2nb - Takes a graph-based neighbor object
      • sym = FALSE says don’t add links to create symmetry
        • No symmetry means if node A is a neighbor of node B, that doesn’t necessarily mean that node B is a neighbor of node A
      • sym = TRUE will insert links to restore symmetry, but the graphs then no longer exactly fulfil their neighbour criteria.
    • grid2nb - Takes GridTopology class object (?)
      • Maybe these are like H3 hexagonal grids
    • knn2nb - Takes a k-NN object
      • sym = FALSE says don’t add links to create symmetry
        • No symmetry means if node A is a neighbor of node B, that doesn’t necessarily mean that node B is a neighbor of node A
        • In the overwhelming majority of cases, k-NN leads to asymmetric neighbours
      • is.symmetric.nb can be used to check for symmetry
    • poly2nb - Takes a sf object with (multi-)polygons or a list of polygon objects with class SpatialPolygon
      • Builds a neighbours list based on regions with contiguous boundaries, that is sharing one or more boundary point.
      • snap allows the shared boundary points to be a short distance from one another.
        • e.g. A narrow body of water separates the boundaries where there’s a ferry or a bridge that could in essence make the boundaries contiguous.
        • Sometimes there are geographical artefacts present which screw up the algorithm detecting continguous boundaries. By increasing the snap value, you can absorb the artefacts and detect the contiguous boundary between the shapes.
          • There is also an edit function to interactively add missing neighbor links.
        • Defaults
          • For SpatialPolygons objects and sf objects with no coordinate reference system, it’s 1.490116e-08 whichs is sqrt(.Machine$double.eps)
          • For sf objecst with coordinate reference systems, it’s 1e-7 (approx 10mm) that’s converted to units of the coordinate system.
      • If queen = TRUE, then when three or more polygons meet at a single point, they all meet the contiguity condition, giving rise to crossed links.
      • If queen = FALSE, (aka rook), at least two boundary points must be within the snap distance of each other
    • tri2nb - Takes a coordinates matrix (e.g. centroids) and is the input for soi.graph

Spatial Weights

  • A spatial weights matrix defines how closely related each pair of nodes are
  • nb2listw will add spatial weights to your neighbors list
  • nb2listwdist - Supplements nb2listw with additional options
    • Defaults: type = “idw”, alpha = 1, style = “raw” (i.e. no normalization)
    • If both type and style are specified, I’d guess that normalization is applied to the weights and not the distances. (i.e. first type applied, then style)
    • Types
      • Inverse Distance Weighting (IDW)
        \[w_{ij} = d_{ij}^{-\alpha}\]
        • IDW weights show extreme behaviour close to 0 and can take on the value infinity. In such cases, the infinite values are replaced by the largest finite weight present in the weights list.
      • Double-Power Distance Weights
        \[w_{ij} = e^{-\alpha \cdot d_{ij}}\]
      • Exponential Distance Decay
        \[w_{ij} = \left[1 - \left(\frac{d_{ij}}{d_{\textrm{max}}}\right)^{\alpha}\right]^{\alpha}\]
  • Normalization Styles
    • Row-Standardized (W)
      • Each row is standardized to sum to 1
        • All the values describing a node’s relationship to each other node will sum to 1
      • Each weight has had its raw value divided by the sum of the row.
      • Most popular as it makes results comparable, i.e. one node’s set of relationships is comparable to another node’s set of relationships (rows)
      • Best when the number of neighbors for each node can vary significantly.
      • Example: Analyzing how house prices are influenced by neighboring houses in a suburban area. The number of neighboring houses isn’t what primarily influences a house’s value, it’s the local houses themeselves.
      • Example: k-NN w/k=2
        \[ \begin{array}{c|cccc} & A & B & C & D \\ \hline A & 0 & 0.66 & 0.34 & 0 \\ B & 0.50 & 0 & 0.50 & 0 \\ C & 0 & 0.61 & 0 & 0.39 \\ D & 0 & 0.28 & 0.72 & 0 \end{array} \]
    • Binary (B)
      • Neighbor/Not Neighbor (1/0)
      • Ignores strength of the link
      • Example: Studying an invasive species. It only matters whether the species is able to or not able to invade another node.
    • Globally Standardized (C)
      • All cells in the matrix are standardized to sum to 1
      • Accounts for global pattern
      • Example: Investingating voting patterns in densely populated districts vs. sparsely populated districts in a state or region. Here you want the total influence to be standardized across the entire state or region.
    • Unstandardized (U)
      • Just uses raw weight values (e.g. distances)
      • Good when actual distances matter and not the relative distances
      • Preserves absolute differences
      • Problematic if distances vary greatly
      • Example: Modeling air pollution dispersion from industrial sites. It’s a physical phenomenon saw distances matter as pollution concentration could decay exponentiall with distance from the site.
    • Variance-Stabilizing
      • Each raw weight is divided by square root of row sums
      • More robust to outliers or extreme values
      • Example: Analyzing disease clusters in areas with very uneven population density. Variance stabilization helps prevent false positives in dense areas
    • Min/Max
      • Divides the weights by the minimum of the maximum row sums and maximum column sums of the input weights
      • Similar to U and C styles

Neighbor Algorithms

  • Graph-based

    • Misc

      • No option to use Great Circle distances for geographical coordinates, only Euclidean distance (planar)
      • All the graph-based neighbour schemes always ensure that all the points will have at least one neighbour.

    • Relative Neighbor Graph (RNG)

      \[ d(x,y) \le \min\{\;\max\{d(x,z),d(y,z)\}\;|\; z \in S\;\} \]

      • Neighbors are defined such that two points \(x\) and \(y\) are connected if the direct distance \(d(x,y)\) is less than or equal to the minimum of the maximum distances from \(x\) and \(y\) to any third point \(z \in S\)
      • Does Not guarantee symmetry

    • Gabriel Graph (GG)

      \[ d(x,y) \le \min\{(d(x,z)^2 + d(y,z)^2)^{1/2} \;|\;z \in S\} \]

      • Neighbors \(x\) and \(y\) are connected if the distance \(d(x, y)\) is less than or equal to the square root of the summ of squared distances from \(x\) and \(y\) to any third point \(z \in S\)
      • Does NOT guarantee symmetry

    • Sphere of Influence Graph (SOI)

      • For a point set \(S\), \(x\) and \(y\) are connected if their respective “spheres of influence” (circles centered at \(x\) and \(y\) with radii equal to the distance to their nearest neighbors) intersect in at least two places
      • Guarantees symmetry

    • Hierarchical Relationship: RNG \(\subseteq\) GG \(\subseteq\) SOI

      • All the links made by RNG will be made by GG, and all the links made by GG will be made by SOI
      • RNG is the most restrictive while SOI is the least.

    • Example: SOI and GG (source)

      library(spdep)

NY8_sf <- 
  st_read(system.file(
            "shapes/NY8_bna_utm18.gpkg", 
            package = "spData"), 
          quiet = TRUE)
# validate geometries
table(st_is_valid(NY8_sf))
#> TRUE 
#>  281 

dplyr::glimpse(NY8_sf)
#> Rows: 281
#> Columns: 13
#> $ AREAKEY    <chr> "36007000100", "36007000200", "36007000300", "36007000400", "3600700…
#> $ AREANAME   <chr> "Binghamton city", "Binghamton city", "Binghamton city", "Binghamton…
#> $ X          <dbl> 4.069397, 4.639371, 5.709063, 7.613831, 7.315968, 8.558753, 9.206733…
#> $ Y          <dbl> -67.3533, -66.8619, -66.9775, -65.9958, -67.3183, -66.9344, -67.1789…
#> $ POP8       <dbl> 3540, 3560, 3739, 2784, 2571, 2729, 3952, 993, 1908, 948, 1172, 1047…
#> $ TRACTCAS   <dbl> 3.08, 4.08, 1.09, 1.07, 3.06, 1.06, 2.09, 0.02, 2.04, 0.02, 1.03, 3.…
#> $ PROPCAS    <dbl> 0.000870, 0.001146, 0.000292, 0.000384, 0.001190, 0.000388, 0.000529…
#> $ PCTOWNHOME <dbl> 0.32773109, 0.42682927, 0.33773959, 0.46160483, 0.19243697, 0.365178…
#> $ PCTAGE65P  <dbl> 0.14661017, 0.23511236, 0.13800481, 0.11889368, 0.14157915, 0.141077…
#> $ Z          <dbl> 0.14197, 0.35555, -0.58165, -0.29634, 0.45689, -0.28123, -0.24605, 0…
#> $ AVGIDIST   <dbl> 0.2373852, 0.2087413, 0.1708548, 0.1406045, 0.1577753, 0.1726033, 0.…
#> $ PEXPOSURE  <dbl> 3.167099, 3.038511, 2.838229, 2.643366, 2.758587, 2.848411, 2.951257…
#> $ geom       <MULTIPOLYGON [m]> MULTIPOLYGON (((421808.5 46..., MULTIPOLYGON (((421794.…

# calculate centroids in counties that will be nodes
NY8_ct_sf <- 
  st_centroid(st_geometry(NY8_sf), 
              of_largest_polygon = TRUE)
class(NY8_ct_sf)
#> [1] "sfc_POINT" "sfc" 
coords_ct <- st_coordinates(NY8_ct_sf)
class(coords_ct)
#> [1] "matrix" "array" 
      # convert point list to neighbor list
NY84_nb <- tri2nb(coords = NY8_ct_sf)
# fit the soi graph and convert graph obj to a neighbor list
NY85_nb_soi <- 
  graph2nb(soi.graph(tri.nb = NY84_nb, 
                     coords = NY8_ct_sf))
summary(NY85_nb_soi)
#> Neighbour list object:
#> Number of regions: 281 
#> Number of nonzero links: 1238 
#> Percentage nonzero weights: 1.567863 
#> Average number of links: 4.405694 
#> 2 disjoint connected subgraphs
#> Link number distribution:
#> 
#>  1  2  3  4  5  6  7  8 
#>  4 29 45 64 70 49 19  1 
#> 4 least connected regions:
#> 228 231 246 247 with 1 link
#> 1 most connected region:
#> 133 with 8 links    

NY85_nb_gg <- 
  graph2nb(gabrielneigh(coords = NY8_ct_sf))
summary(NY85_nb_gg)
#> Neighbour list object:
#> Number of regions: 281 
#> Number of nonzero links: 592 
#> Percentage nonzero weights: 0.7497372 
#> Average number of links: 2.106762 
#> 20 regions with no links:
#> 35, 51, 55, 67, 78, 82, 109, 190, 210, 212, 219, 234, 235, 241, 243, 251, 277, 278, 279, 281
#> Non-symmetric neighbours list
#> Link number distribution:
#> 
#>   0   1   2   3   4   5 
#>  20  68 105  48  30  10 
#> 68 least connected regions:
#> 10 16 18 27 30 31 32 33 34 45 46 48 49 50 56 64 66 73 77 81 89 90 91 94 100 104 107 108 123 146 149 153 160 161 164 167 168 179 189 194 202 209 214 215 220 222 223 231 232 240 242 246 247 248 249 250 255 256 257 258 260 262 263 271 272 275 276 280 with 1 link
#> 10 most connected regions:
#> 37 41 58 63 70 102 112 114 184 239 with 5 links
      • There are two neighbor list conversions:
        • tri2nb returns a special list required as input for soi.graph. Also, I think {dbscan} is required to be installed for soi.graph but maybe not the others.
        • graph2nb converts a graph object to a neighbor list that’s used for graphing the network
      • The RNG method (relativeneigh) is fit the same way as the GG method.

       par(mfrow = c(1, 2))
plot(st_geometry(NY8_sf), border = "gray")
plot(NY85_nb_soi,
     coords = coords_ct,
     add = TRUE)
title(main = "Sphere of Influence")

# plot boundaries
plot(st_geometry(NY8_sf), border = "gray")
# plot edges and nodes
plot(NY85_nb_gg, 
     coords = coords_ct, 
     add = TRUE)
title(main = "Gabriel Graph")
      • I thought the difference would be more apparent between the two methods, but they’re pretty similar.
      • I feel the GG graph is more connected overall, but the SOI is more connected in areas where the nodes are denser.
  • k-NN

    • Does NOT guarantee symmetry (almost always asymmetric)

    • Example: (source)

      NY88_nb_sf <- 
  knn2nb(knearneigh(NY8_ct_sf, 
                    k = 4))

# plot boundaries
plot(st_geometry(NY8_sf), border="gray")
# plot edges and nodes
plot(NY88_nb_sf,
     coords = coords_ct, 
     add = TRUE)
title(main="K nearest neighbours, k = 4")

      • See Graph-based >> Example for code for NY8_sf, NY8_ct_sf, and coords_ct

        • Where NY8_ct_sf is a point list of county centroids and coords_ct is the same thing but in a point matrix

      • knn2nb coverts the knn graph object to a neighbor list for graphing

      • If longlat = TRUE, Great Circle distances in kilometers are used (See DIstance Neighbors >> Example 2)

        # Convert to geographic coordinates
NY8_ct_ll <- st_transform(NY8_ct_sf, 4326)
st_is_longlat(NY8_ct_ll)
#> [1] TRUE

      • For larger datasets, changing the engine to S2 (spatial indexing) along with the coordinates being geographical, spherical distances are calculated which can be an acceptable compromise between accuracy and speed

        sf_use_s2(TRUE)
pts_ll1_nb <- knn2nb(knearneigh(NY8_ct_ll, k = 4))
  • Distance Neighbors

    • Identifies neighbors within a euclidean (default) distance range using a k-NN graph

      • So, larger the upper threshold, then more links will be made.
      • This fraction could correspond to a “reasonable” walking or driving distance if you’re studying neighborhood effects.

    • Example 1: (source)

      dsts <- unlist(nbdists(nb = NY88_nb_sf, 
                       coords = NY8_ct_sf))
max_1nn <- max(dsts)
max_1nn
#> [1] 26564.68

NY810_nb <- 
  dnearneigh(NY8_ct_sf, 
             d1 = 0, 
             d2 = 0.45 * max_1nn)

# plot boundaries
plot(st_geometry(NY8_sf), 
     border="grey", 
     reset=FALSE,
     main = paste0("Distance based neighbours 0 to ",  
                   format(0.45 * max_1nn), " m")
)
# plot edges and nodes
plot(NY810_nb, 
     coords_ct, 
     add = TRUE)
      • nbdists returns the Euclidean distances along the links of k-NN graph
        • Where NY88_nb_sf is the neighbor list of the k-NN graph object (see k-NN example) and NY8_ct_sf and coords_ct are the point list and point matrix of county centroids respectively (see Graph-based example)
        • The max of these distances is 26,564.68 meters or 26.6 km
      • The 75th percentile of the max of those distances is used as the upper threshold for the distance neighbors algorithm.
      • If longlat = TRUE, then Great Circle distance in kilometers is used (See Example 2)
      • If x is an “sf” object, coordinates are geographical, and use_s2 = TRUE (spatial indexing), spherical distances in kilometers are used.
        • See this vignette section for a discussion on this setting and dwithin
        • sf_use_s2(TRUE) might also need to be set

    • Example 2: Geographical Distances

      ny_sf <- 
  st_read(system.file(
    "shapes/NY8_bna_utm18.gpkg", 
    package = "spData"), 
    quiet = TRUE)

ny_sf_ll <- st_transform(ny_sf, 4326)

dplyr::glimpse(ny_sf_ll)
#> Rows: 281
#> Columns: 13
#> $ AREAKEY    <chr> "36007000100", "36007000200", "36007000300", "36007000400", "36007000500", "…
#> $ AREANAME   <chr> "Binghamton city", "Binghamton city", "Binghamton city", "Binghamton city", …
#> $ X          <dbl> 4.069397, 4.639371, 5.709063, 7.613831, 7.315968, 8.558753, 9.206733, 10.180…
#> $ Y          <dbl> -67.3533, -66.8619, -66.9775, -65.9958, -67.3183, -66.9344, -67.1789, -66.87…
#> $ POP8       <dbl> 3540, 3560, 3739, 2784, 2571, 2729, 3952, 993, 1908, 948, 1172, 1047, 3138, …
#> $ TRACTCAS   <dbl> 3.08, 4.08, 1.09, 1.07, 3.06, 1.06, 2.09, 0.02, 2.04, 0.02, 1.03, 3.02, 5.07…
#> $ PROPCAS    <dbl> 0.000870, 0.001146, 0.000292, 0.000384, 0.001190, 0.000388, 0.000529, 0.0000…
#> $ PCTOWNHOME <dbl> 0.32773109, 0.42682927, 0.33773959, 0.46160483, 0.19243697, 0.36517857, 0.66…
#> $ PCTAGE65P  <dbl> 0.14661017, 0.23511236, 0.13800481, 0.11889368, 0.14157915, 0.14107732, 0.23…
#> $ Z          <dbl> 0.14197, 0.35555, -0.58165, -0.29634, 0.45689, -0.28123, -0.24605, 0.02683, …
#> $ AVGIDIST   <dbl> 0.2373852, 0.2087413, 0.1708548, 0.1406045, 0.1577753, 0.1726033, 0.1912999,…
#> $ PEXPOSURE  <dbl> 3.167099, 3.038511, 2.838229, 2.643366, 2.758587, 2.848411, 2.951257, 2.9833…
#> $ geom       <MULTIPOLYGON [°]> MULTIPOLYGON (((-75.9458 42..., MULTIPOLYGON (((-75.946 42....,…

# calculate centroids in counties that will be nodes
ny_ct_ll <- 
  st_centroid(st_geometry(ny_sf_ll), 
              of_largest_polygon = TRUE)
st_is_longlat(ny_ct_ll)
#> [1] TRUE

# matrix format needed for plots
coords_ct_ll <- st_coordinates(ny_ct_ll)
      • Since we’re using geographical coordinates in our distance and centroid calcuations our boundaries have to be in the same coordinate system when plotting
      • If we weren’t worried about plotting, then st_tranform could’ve been used on the centroids object instead of the dataframe.
      # knn w/longlat = TRUE
ny_nb_ll <- 
  knn2nb(knearneigh(ny_ct_ll, 
                    k = 4,
                    longlat = TRUE))
summary(ny_nb_ll)
#> Neighbour list object:
#> Number of regions: 281 
#> Number of nonzero links: 1124 
#> Percentage nonzero weights: 1.423488 
#> Average number of links: 4 
#> Non-symmetric neighbours list
#> Link number distribution:
#> 
#>   4 
#> 281 
#> 281 least connected regions:
#> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 with 4 links
#> 281 most connected regions:
#> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 with 4 links
# Get maximum neighbor distance
dsts_ll <- unlist(nbdists(nb = ny_nb_ll, 
                          coords = ny_ct_ll))
max_1nn <- max(dsts_ll)
max_1nn
#> [1] 32.04742

# neighbors within range
ny_dn_ll <- 
  dnearneigh(ny_ct_ll, 
             d1 = 0, 
             d2 = 0.005 * max_1nn, 
             longlat = TRUE)
summary(ny_dn_ll)
#> Neighbour list object:
#> Number of regions: 281 
#> Number of nonzero links: 16078 
#> Percentage nonzero weights: 20.36195 
#> Average number of links: 57.21708 
#> 1 region with no links:
#> 30
#> 2 disjoint connected subgraphs
#> Link number distribution:
#> 
#>   0   1   2   3   4   5   6   7   8   9  10  11  13  14  15  16  18  19  20  21  23  24  25  27  28  29  30  31  32  33  34  35  37  38  39  40  41  42  43  44  45  46  48  49  50  51  59  63  65  66  67 
#>   1   5   5  10   9   6   5   7   5   9   7   1   5   3   3   2   5   5   7   4   1   1   1   1   2   1   1   1   1   2   3   1   1   3   1   3   8   4   3   1   7   7   1   1   1   1   1   1   2   1   2 
#>  74  77  79  80  82  87  88  89  94  96  97  98 100 101 102 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 
#>   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   3   2   5   4   8  10   5  17  14   9   7   8   2 
#> 5 least connected regions:
#> 56 75 106 109 258 with 1 link
#> 2 most connected regions:
#> 112 122 with 119 links
      • longlat = TRUE was set in both knearneigh and dnearneigh

      # boundaries
plot(st_geometry(ny_sf_ll), 
     border="grey", 
     reset = FALSE,
     main = paste0("Distance based neighbours 0 to ", 
                   format(round(0.005 * max_1nn, 2)), " km"))
# nodes and edges
plot(ny_dn_ll, 
     coords_ct_ll,
     add = TRUE)
      • Notice the distance is in kilometers and not meters