Multilevel, Longitudinal

Misc

• Also see Mixed Effects, General >> Considerations >> Variable Assignment
• Need to figure out if
  • There’s significant within-unit variation. If so, then FE model will likely be the best model
    • Article with simulated data showed that within variation around sd < 0.5 didn’t detect the effect of explanatory variable but ymmv (depends on # of units, observations per unit, N)
  • There’s significant between-unit variation. If so, then RE model will likely be the best model

Multilevel

• Misc
  • Also see Regression, Ordinal >> EDA >> Crosstabs
  • Is my data clustered?
  • Separate variables into levels
    • Level One: Variables measured at the most frequently occurring observational unit
      • i.e. Variables that (for the most part) have different values for each row
      • i.e. Vary for each repeated measure of a subject and vary between subjects
    • Level Two: Variables measured on larger observational units
      • i.e. Constant for each repeated measure of a subject but vary between each subject

Univariate

• Level 1 and Level 2
  • Group-level correlation or autocorrelation in variables can mislead or obscure patterns
    • If level 2 variable categories are pretty well balanced and there’s sufficient data, then plotting means can remove the correlation affect in the plot
  • Continuous
    • Looking at the skew, median/mean, bimodal or not
    • Example:
      
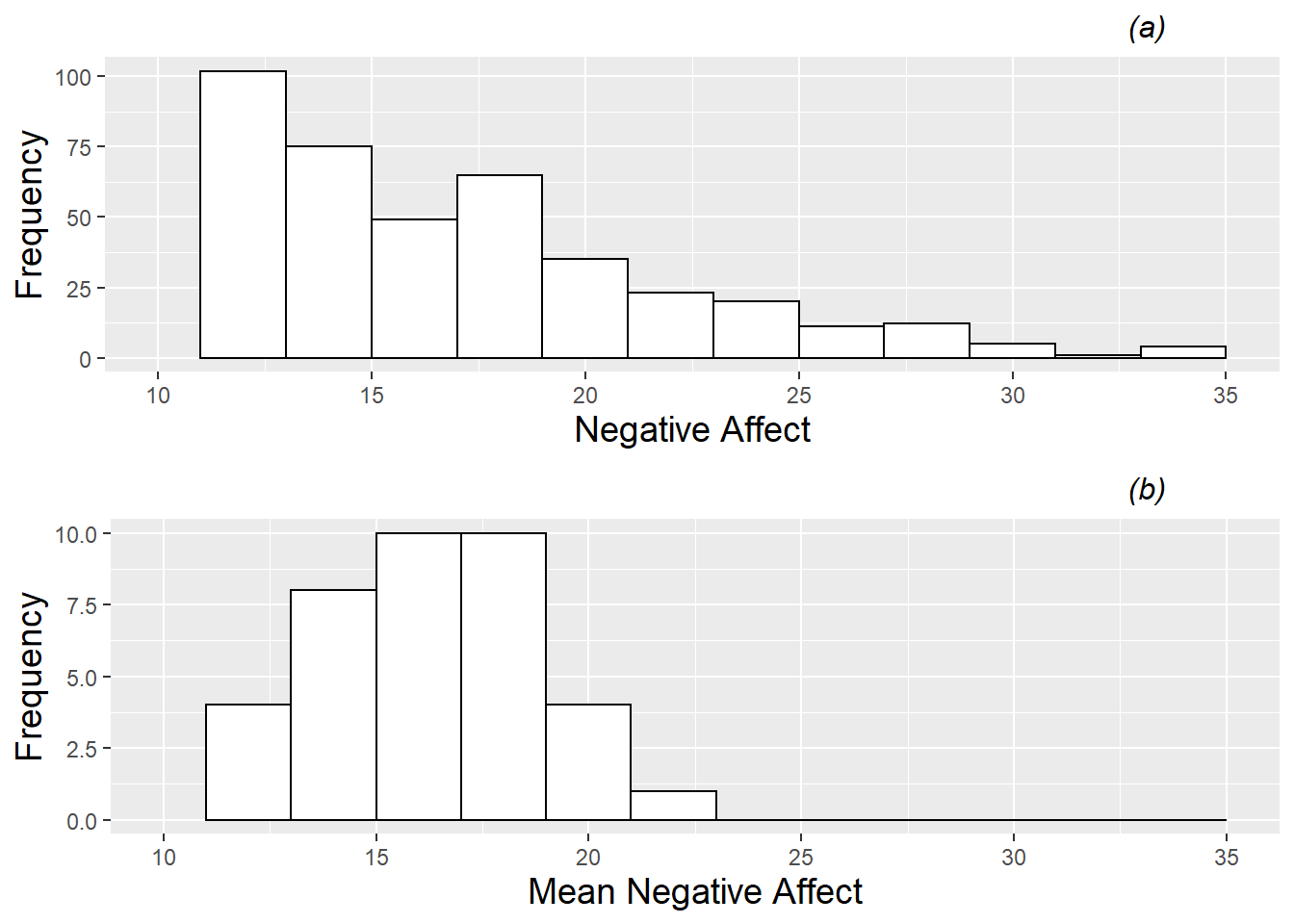
      • (Top) Each observation is plotted as if each observation is independent of the other
        • * Ignores dependency (via repeated measures)
      • (Bottom) Means for each subject or case or other level of a random variable
        • * Removes dependency
      • Interpretation: Right skew remains in both plots but plot 1’s decrease is smoother than plot 2’s
  • Categorical
    • Calculate proportions of each category and noting trends (ordinal variables) or severe imbalances

Bivariate

• Questions
  • Is there is a general trend suggesting that as the covariate increases the response either increases or decreases (trend)
  • Do subjects at certain levels of the covariate tend to have similar mean values of the response (low variability)
  • Is the variation in the response at different levels of the covariate (unequal variability)
• Me: Comparison between plots that take into account dependency and the same plot that doesn’t
  • Trend in plot that ignores dependency but no trend in plot that removes dependency
    • May indicate within-subject variation
  • No trend in plot that ignores dependency but trend in plot that removes dependency
    • May indicate between-subject variation
• Boxplots (Categorical)
  
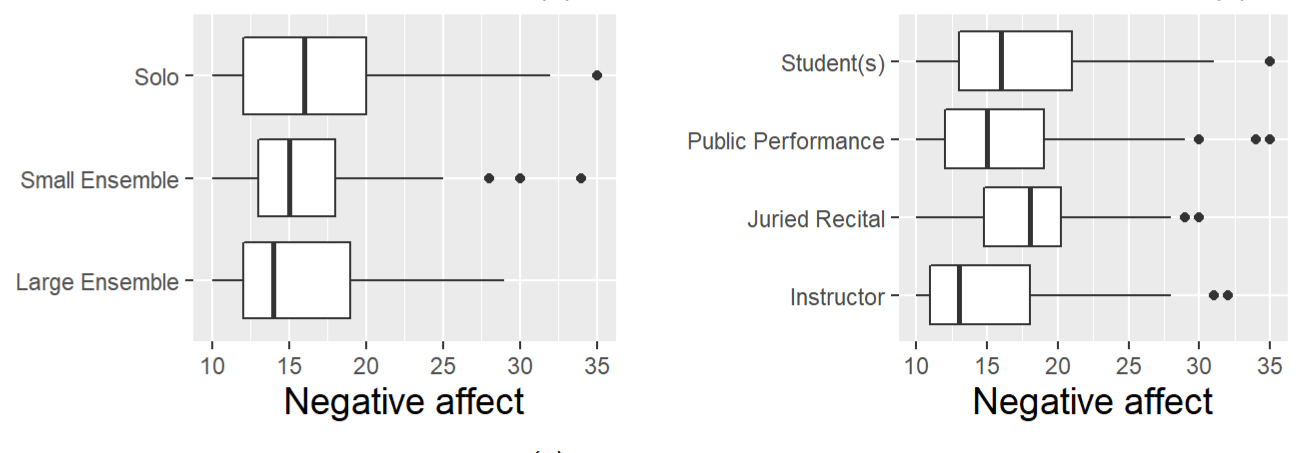
  • Level 1 categorical covariates (y-axis) vs continuous outcome (x-axis)
  • * Ignores dependency (via repeated measures)
  • Interpretation
    • Left: ordinal covariate, medians are close and boxes pretty much contained within each other but there might be a trend
    • Right: Looks like some decent variation between categories
  • Mean outcome (per subject) vs covariate
    
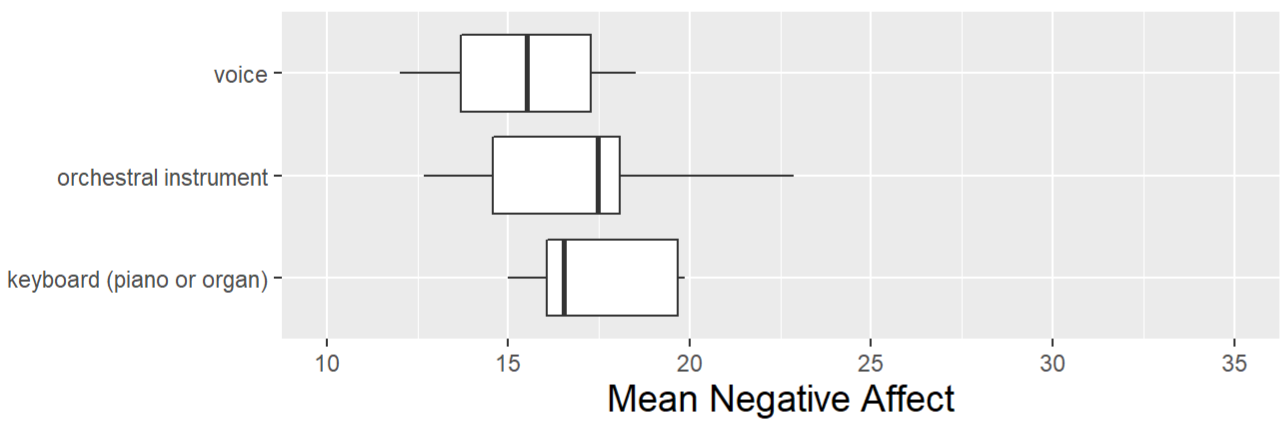
    • * Removes dependency
    • Interpretation: looks like some decent variation between categories
• Scatter (Continuous)
  
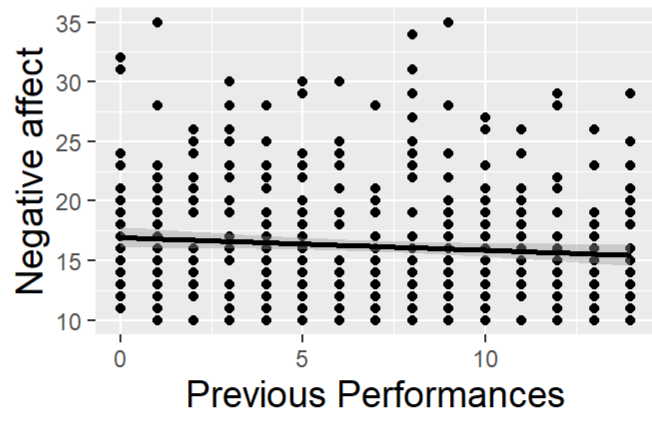
  • Level 1 continuous covariate (x-axis) vs continuous outcome (y-axis)
  • * Ignores dependency (via repeated measures)
  • Actually a discrete  covariate being treated as continuous the fact that does seem to be a small trend is what’s important
  • Mean outcome (per subject) vs covariate
    
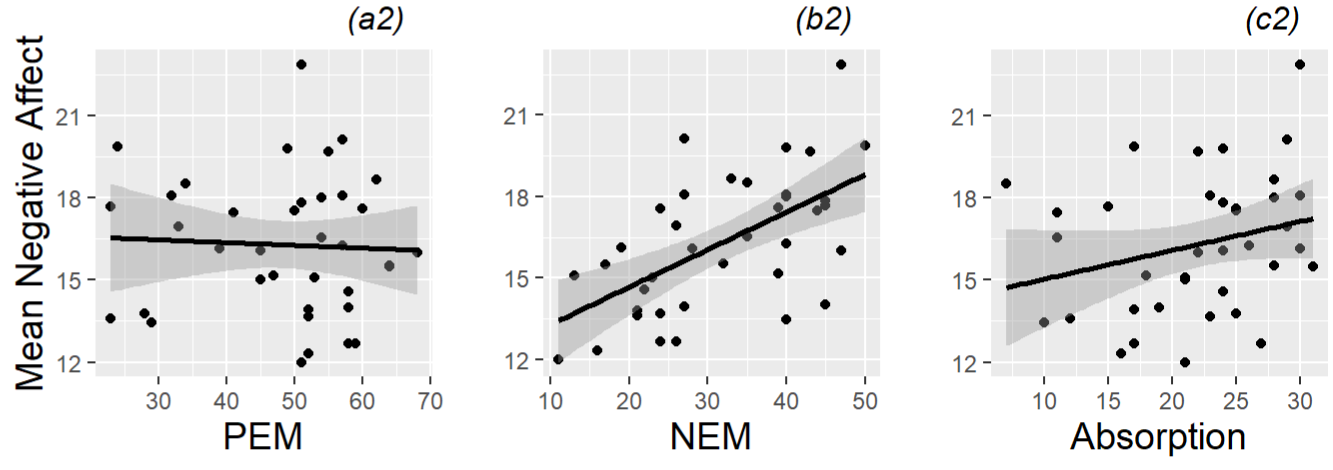
    • * Removes dependency
    • Interpretation: PEM not showing much of an correlation if any
• Facetting previous plots by subject
  
  
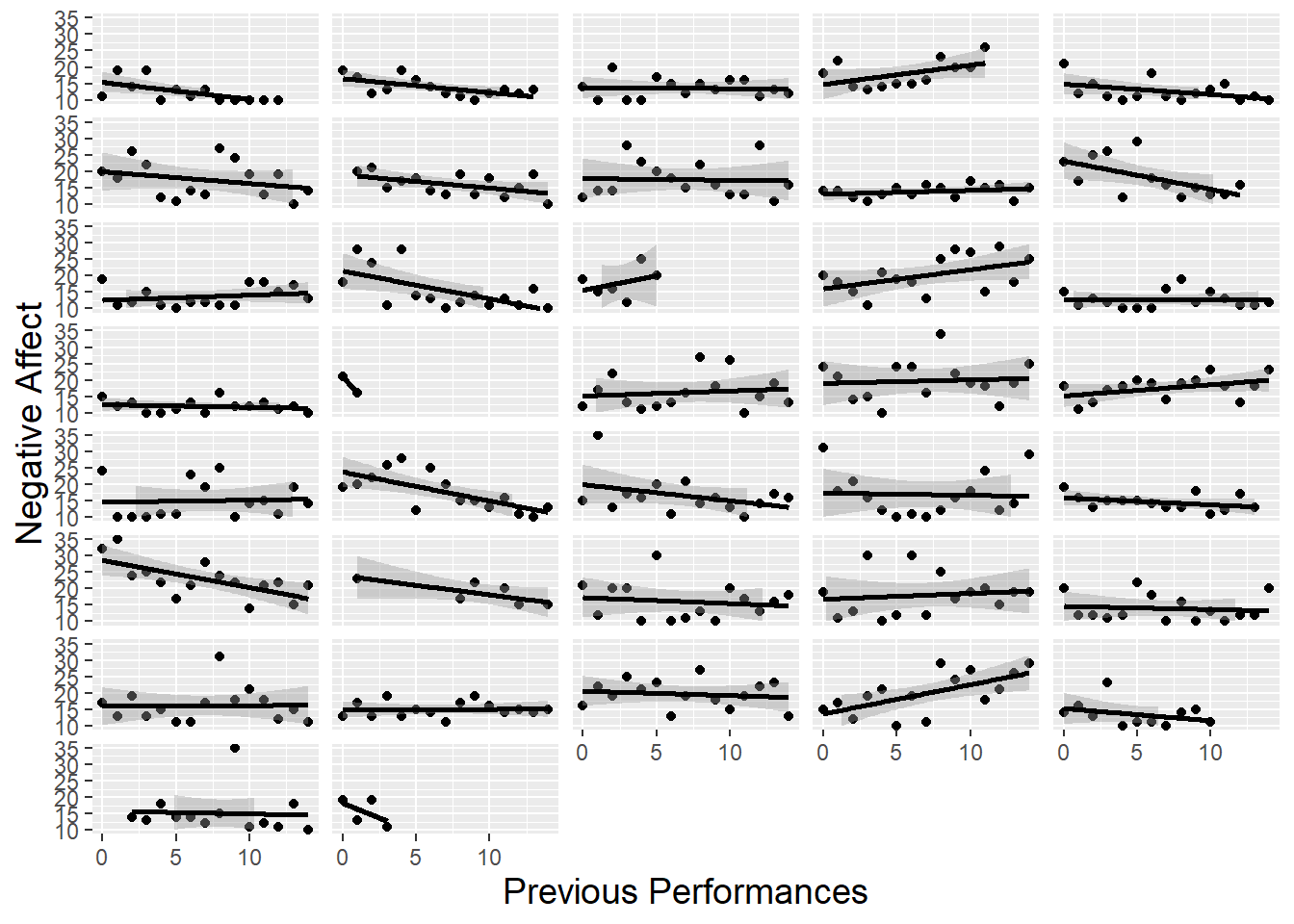
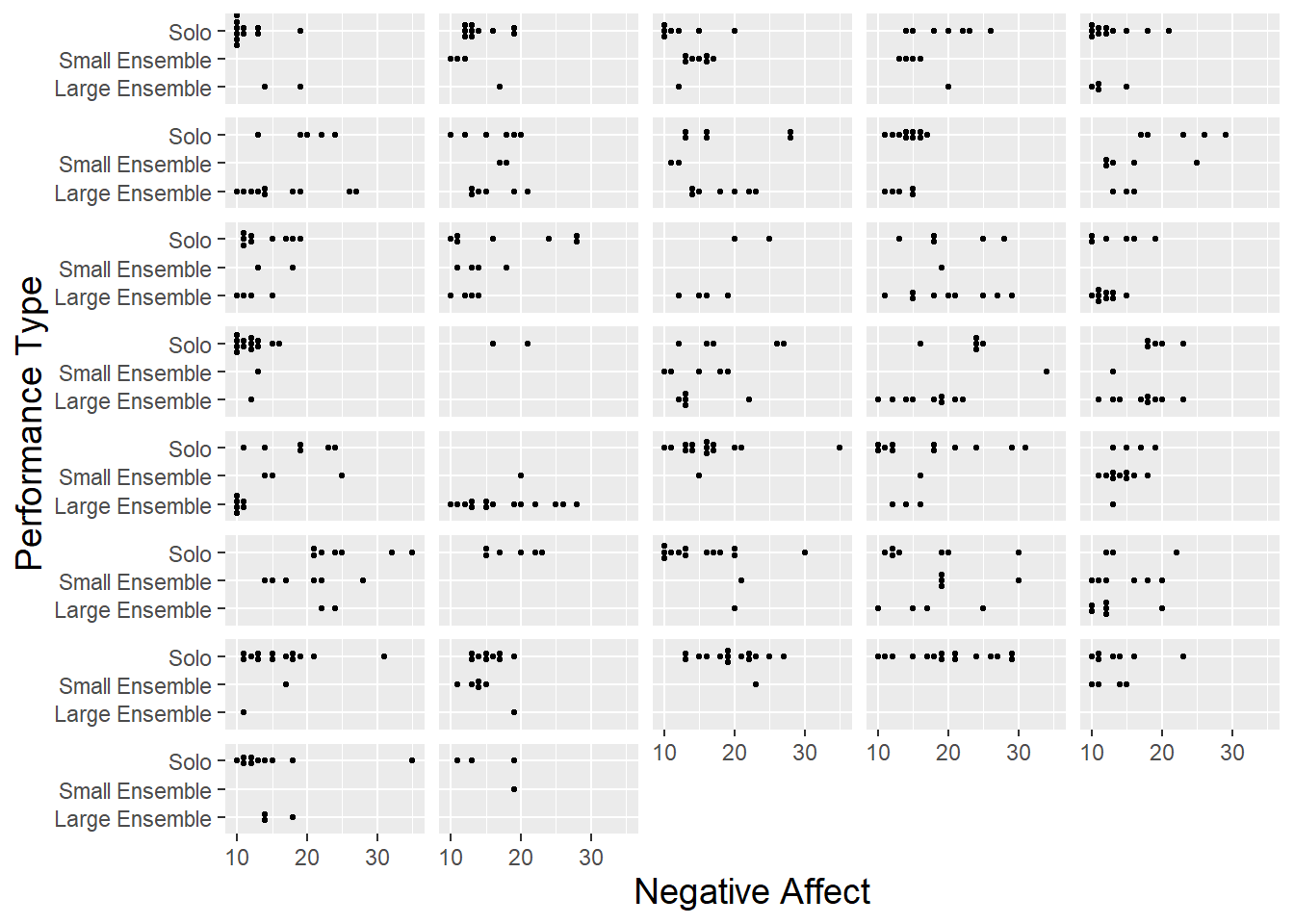
  • Left
    • Mostly downward trends but some upward trends
    • Useful for prior formulation
    • Gives an idea about the uncertainty of the slope of this variable
  • Right
    • Scarcity of points for some categories makes boxplots a bad idea
    • Difficult to spot any trends
  • * Removes dependency

Trivariate

• Scatter, color by random variable
  

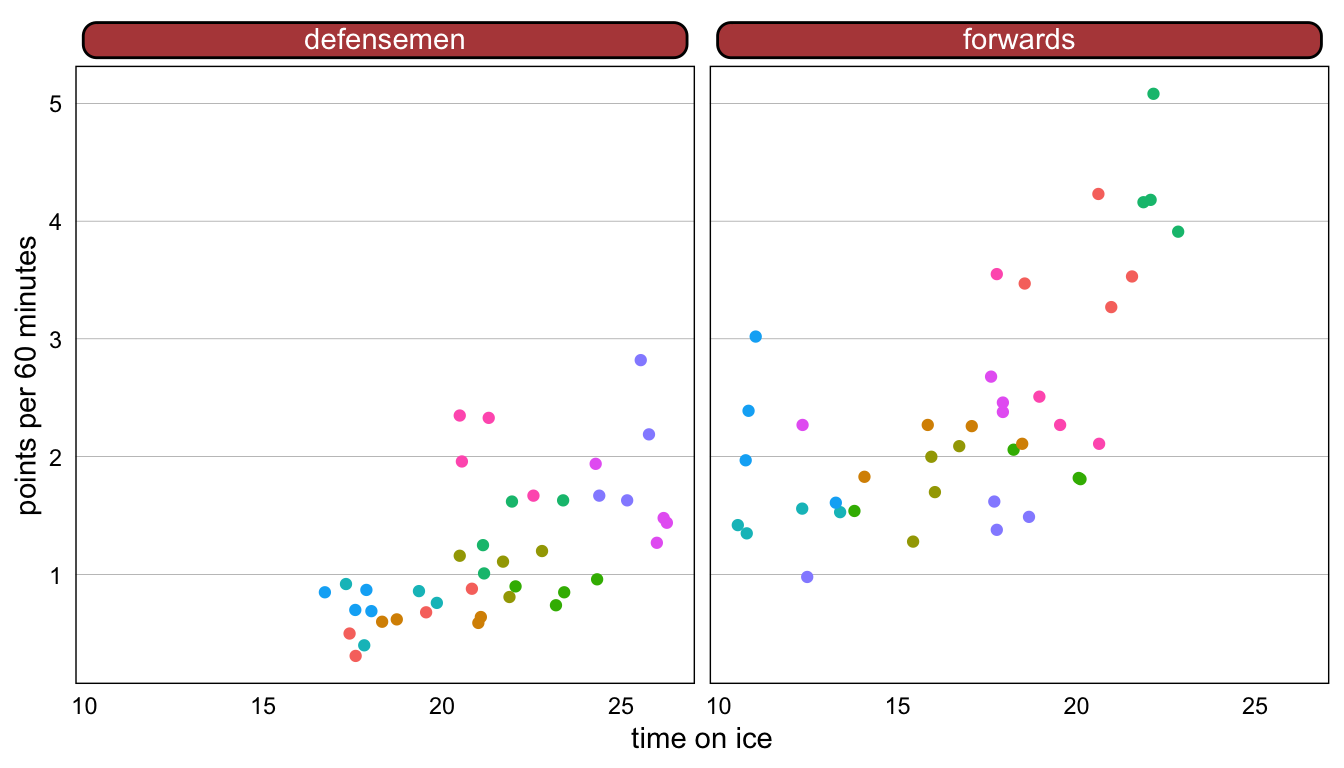
  • Variables
    • “points per 60 min” (outcome)
    • “time on ice” (fixed effect)
    • facetted by “position” (fixed effect)
    • colored by “player” (potential random variable)
  • Interpretation
    • Theres does seem to be clustering by “player” therefore a mixed effects model might be a good choice.

• Scatter with linear smooths (link)
  

  theme_set(theme_classic(base_size = 14))
  ggplot(d, aes(x = NAP, y = log_richness, color = Beach_c)) +
    geom_point() +
    stat_smooth(method = "lm", alpha = 0.1) +
    scale_color_brewer(palette = "Paired")

  • Shows the varying slopes and some varying intercepts (but an overall trend) by random variable, Beach_c

• Null Model (aka random intercept-only model)

  m0 <- 
    lmer(pp60 ~ 1 + (1 | player), 
         data = df)
  
  jtools::summ(m0)
  GROUPING VARIABLES
  GROUP # GROUPS ICC
  player       20      0.89

  • ICC > 0.1 is generally accepted as the minimal threshold for justifying the use of Mixed Effects model (See ICC section)

Longitudinal

• Misc
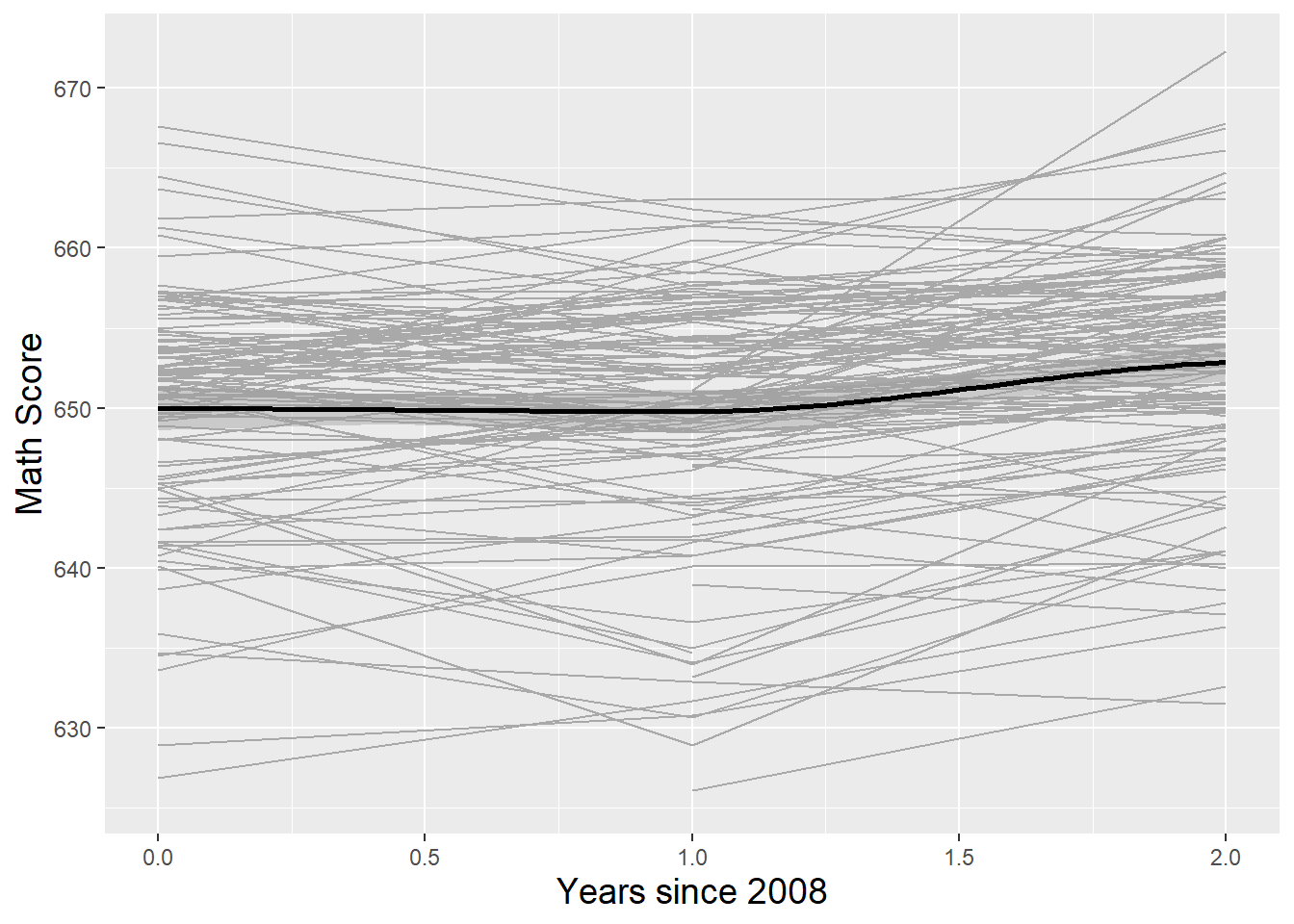
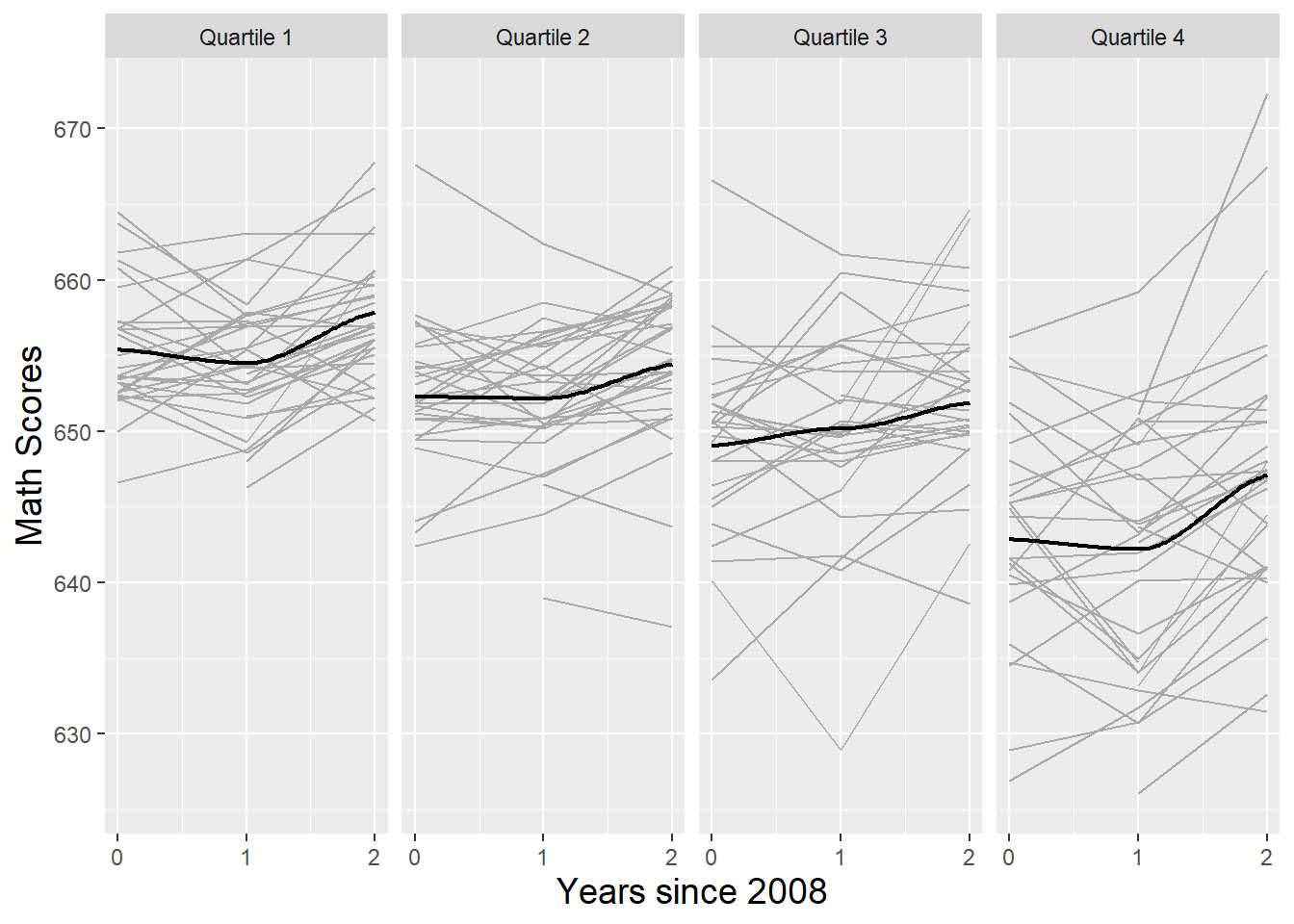
  • Repeated measures that have a sequential or time component
  • packages: {brolgar}

Univariate

• Continuous Outcome vs. Time
  • Facetted by Observational Unit (e.g. school)
    
    
    • Linear Fit and Line Chart
  • Spaghetti
    

Bivariate

• Bold line is the overall fit with LOESS

• Continuous Outcome vs Time

  • Facetted by Categorical
    
  • Facetted by Binned Continuous
    

• Time Endpoints
  

  • “School Type” is a categorical, level 2 variable and “Math Score” is the numeric outcome
  • Looking for change from the initial measurement to the final measurement

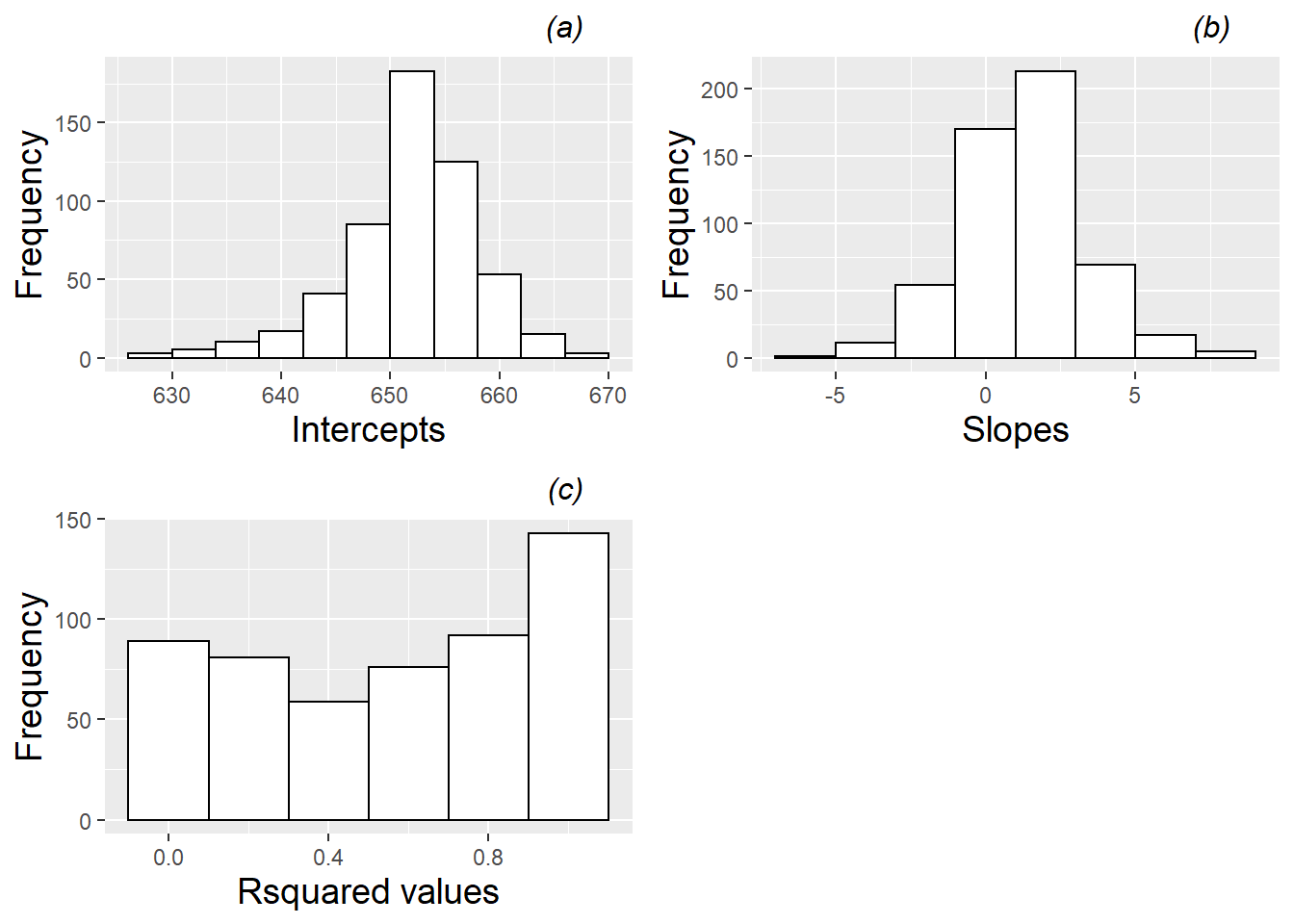
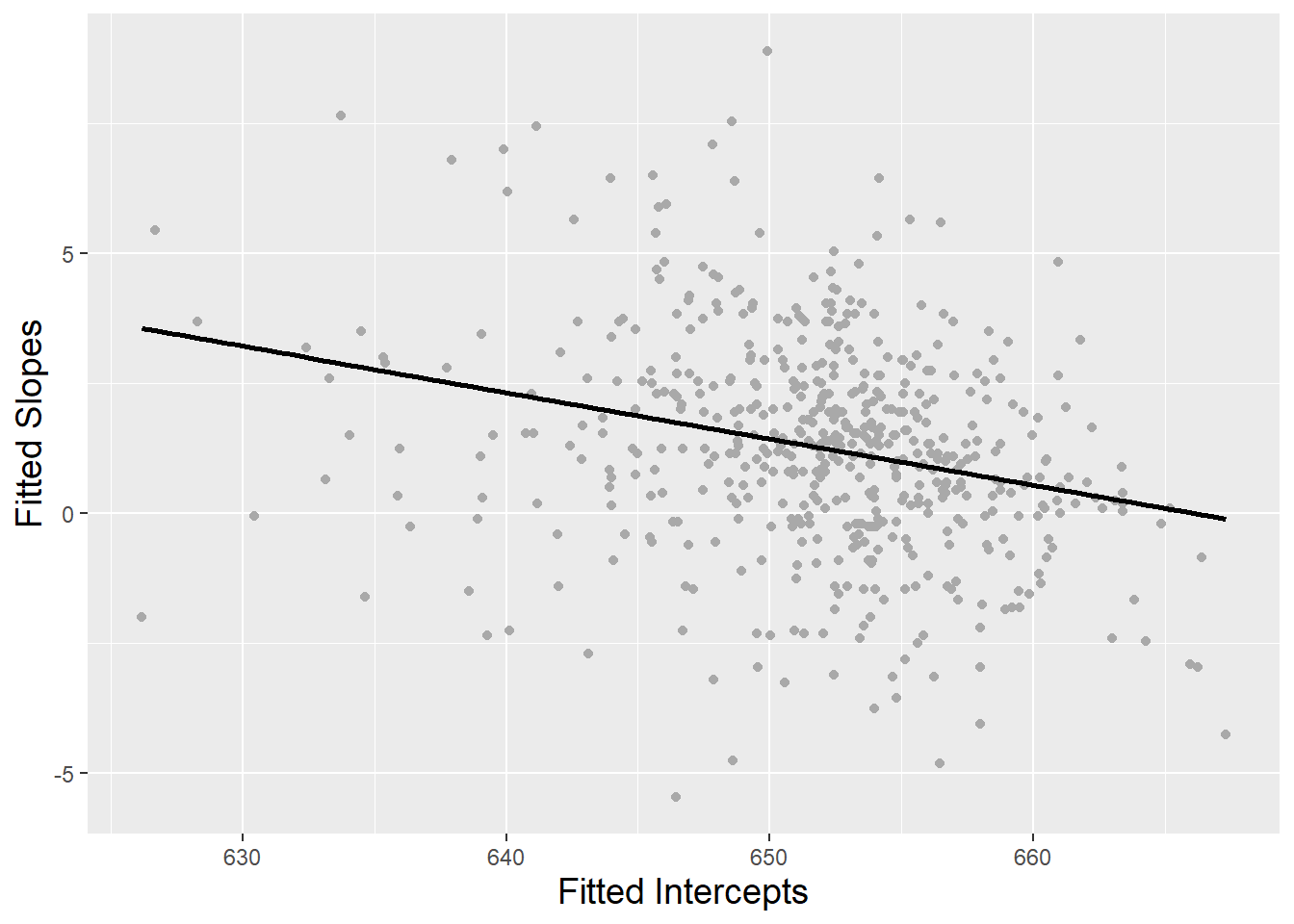
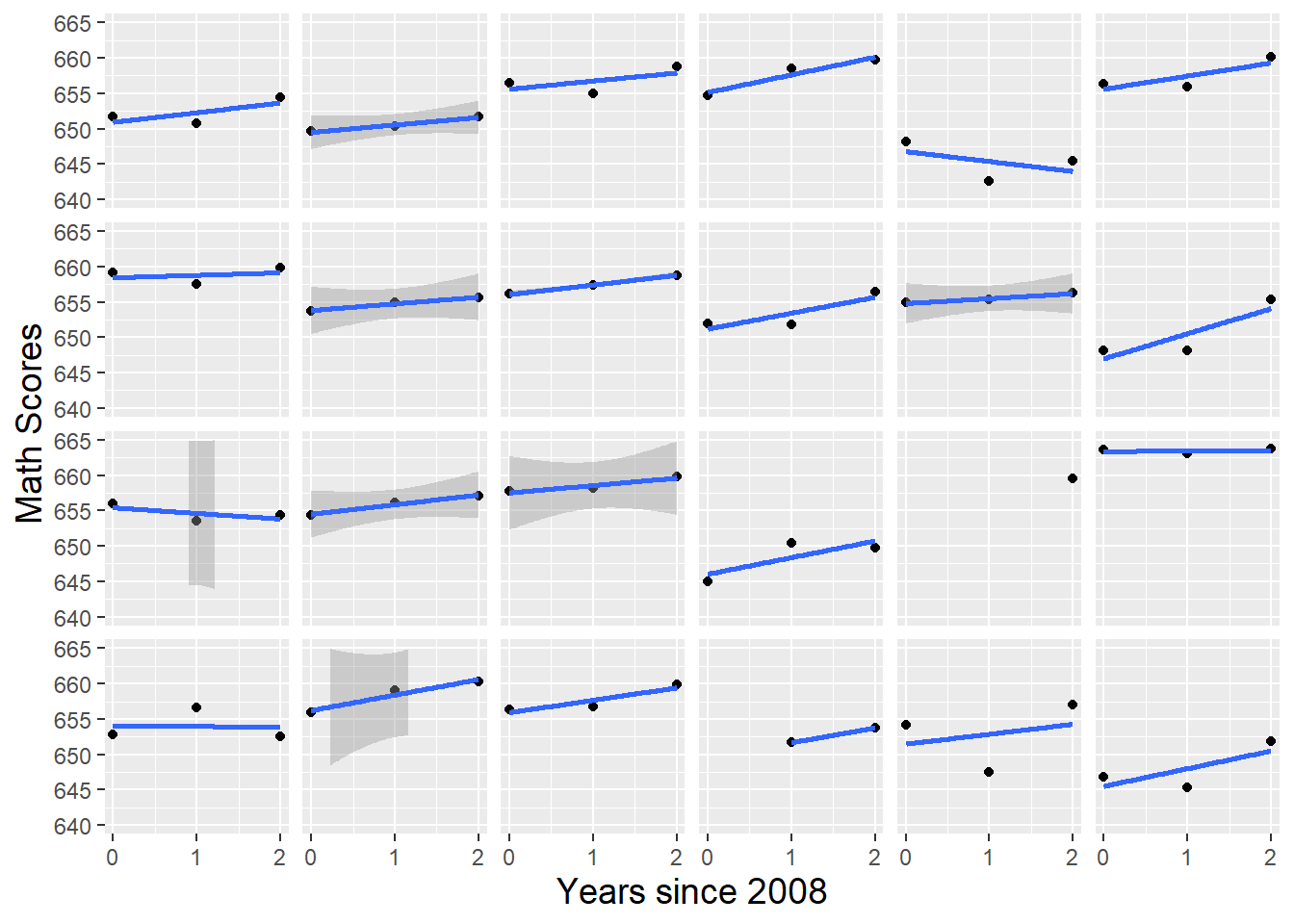
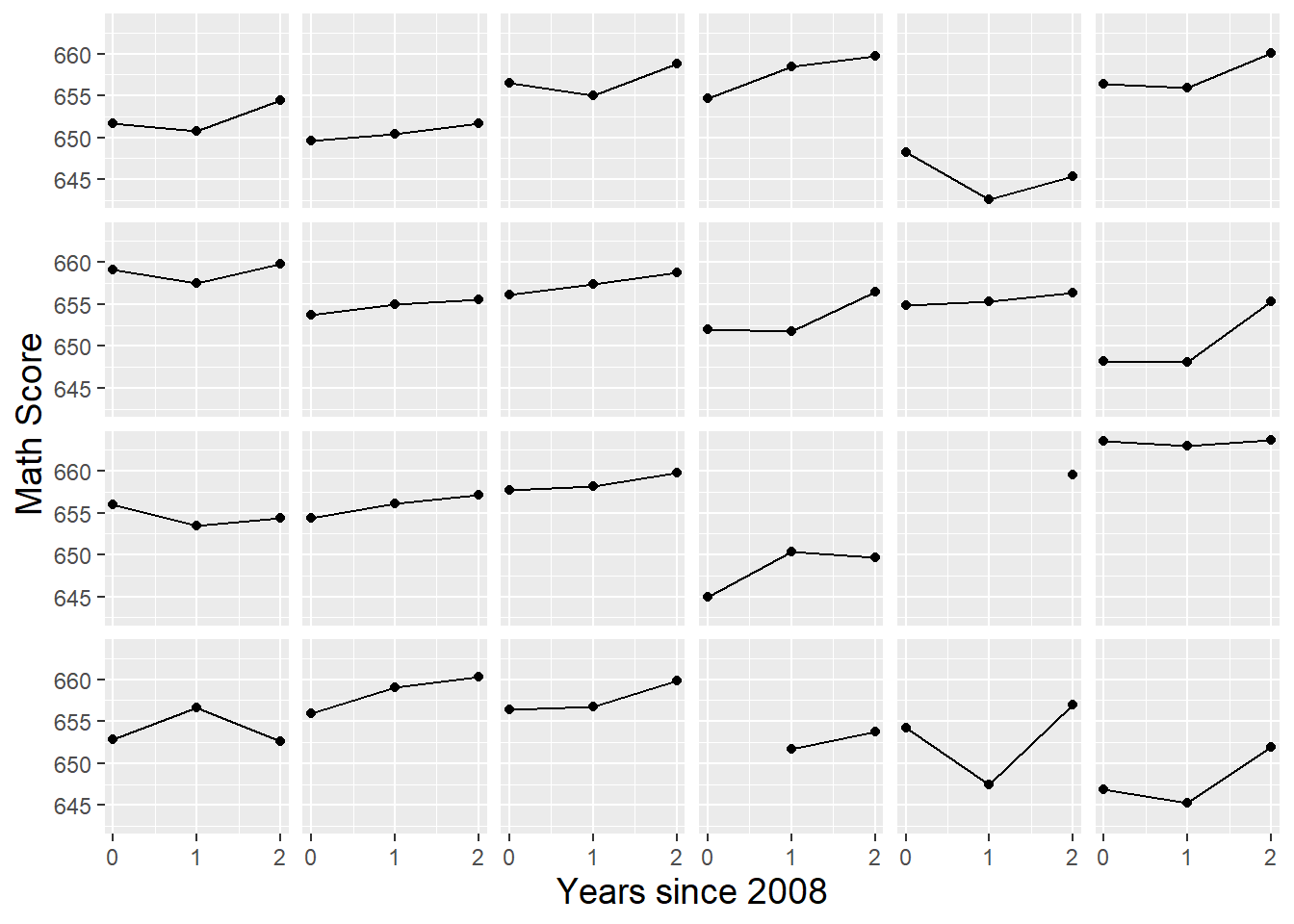
Linear parameters

• Fit a linear regression for each subject/unit with its repeated measurements
  • See univariate >> numerical outcome vs. time >> Facetted by observational unit >> (left) linear fit
• Advantages
  • Each unit’s/subject’s data points can be summarized with two summary statistics—an intercept and a slope
    • Bigger advantage when there are more observations over time per unit/subject
  • Seems like a good way for using empirical bayes (i.e. use these distributions for prior specifications)
• Disadvantages
  • Slopes cannot be estimated for those units/subjects with just a single observation
  • R-squared values cannot be calculated for those units/subjects with no variability in test scores during the time period
  • R-squared values must be 1 for those units/subjects with only two test scores.
• Summary Statistics
  • Mean and SD for intercepts and slopes
• Univariate
  • \(y_t = \beta_0 + \beta_1 t + \epsilon_t\)
    • \(t\) is the time variable (aka trend)
  • Parameter Distributions
    
  • Correlation
    
    • Lower intitial values (intercepts) show the greatest growth (slopes) over time
    • Correlation = -0.32
• Bivariate
  • Process
    • Filter data by Level 2 variable
    • For each category of the Level 2 variable, fit a regression, yt = β0 + β1t + εt, for each unit/subject.
    • Aggregate results
  • Parameter Distributions
    
    • “School Type” is a Level 2, binary variable